Test 3.27 T2 旅行

Description

FGD 想从成都去上海旅游。在旅途中他希望经过一些城市并在那里欣赏风景,品尝风味小吃或者做其他的有趣的事情。经过这些城市的顺序不是完全随意的,比如说 FGD 不希望在刚吃过一顿大餐之后立刻去下一个城市登山,而是希望去另外什么地方喝下午茶。幸运的是,FGD 的旅程不是既定的,他可以在某些旅行方案之间进行选择。由于 FGD 非常讨厌乘车的颠簸,他希望在满足他的要求的情况下,旅行的距离尽量短,这样他就有足够的精力来欣赏风景。整个城市交通网络包含 N 个城市以及城市与城市之间的双向道路 M 条。城市自 1 至 N 依次编号,道路亦然。没有从某个城市直接到它自己的道路,两个城市之间最多只有一条道路直接相连,但可以有多条连接两个城市的路径。任意两条道路如果相遇,则相遇点也必然是这 N 个城市之一,在中途,由于修建了立交桥和下穿隧道,道路是不会相交的。每条道路都有一个固定长度。在中途,FGD 想要经过 K(K<=N-2)个城市。成都编号为 1,上海编号为 N,而 FGD 想要经过的 N 个城市编号依次为 2,3,...,K+1。举例来说,假设交通网络如下图。FGD 想要经过城市 2,3,4,5,并且在 2 停留的时候在 3 之前,而在 4,5 停留的时候在 3 之后。那么最短的旅行方案是1-2-4-3-4-5-8 , 总长度为 19。注意 FGD 为了从城市 2 到城市 4 可以路过城市 3,但不在城市 3 停留。这样就不违反 FGD 的要求了。并且由于 FGD 想要走最短的路径,因此这个方案正是 FGD需要的。

Input

第一行包含 3 个整数 N(2<=N<=20000),M(1<=M<=200000),K(0<=K<=20),意义如上所述。以下 M 行,每行包含 3 个整数 X,Y,Z,(1<=X<y<=n, 1<="Z=1000)表示城市 X与 Y 之间有一条双向道路。你可以认为输入文件使得一定能自成都到上海以及任何 FGD 想要去的城市。"下一行包含一个整数 G(0<=G<=K*(K-1)/2)。以下 G 行,每行包含 2 个整数 X Y,(2<=X,Y<=K+1)表示 FGD 想要在游览城市Y 之前,一定要游览城市 X。你可以认为至少存在一种满足所有限制的游览方案。

Output

只包含一行,包含一个整数,表示最短的旅行距离。

Sample Input

8 15 4

1 2 3

1 3 4

1 4 4

1 6 2

1 7 3

2 3 6

2 4 2

2 5 2

3 4 3

3 6 3

3 8 6

4 5 2

4 8 6

5 7 4

5 8 6

3

2 3

3 4

3 5

Sample Output

Hint

下面对应于题目中给出的例子。

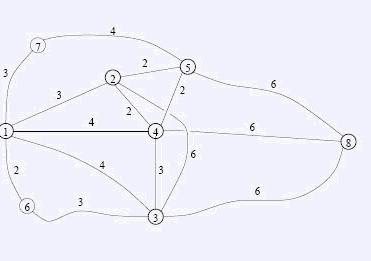
Solution

看到k非常小，就可以想到状态压缩的动态规划(先例：售货员的难题)。设f[i][j]表示经过的1到k+1的点的集合为i，当前所在点为j时的最短路径。那么有如下状态转移方程：

\[f[i|(1<<l)][l]=min(f[i][j]+dis[j][l],f[i|(1<<l)][l])
\]

其中dis[j][l]表示从j到l的最短路径，那么为了判断一个点是否满足其先要访问的点的条件，可以用g[i]表示一个点i的所有前驱节点集合(同样用状态压缩)，如果在状态转移方程中满足i&g[i]=g[i]，就说明可行。dis数组可以用SPFA跑出来。动态规划完成后，由于没有将第n个点计算在内，所以最终的答案为：

\[ans=max(f[1<<k][i]+dis[i][n])_{i=1,2,...,k+1}
\]

另外，为了表示方便和节省空间，第i个点在二进制集合中的位置可设为i-2，这样就可以从第0位开始表示了。

#include <iostream>

#include <cstdio>

#include <queue>

#include <cstring>

#define N 20002

#define M 200002

#define int long long

using namespace std;

int head[N],ver[M*2],nxt[M*2],edge[M*2],l;

int n,m,k,c,i,j,d[22][22],dis[N],f[1048576][22],g[22];

bool in[N];

int read()

{

	char c=getchar();

	int w=0;

	while(c<'0'||c>'9') c=getchar();

	while(c<='9'&&c>='0'){

		w=w*10+c-'0';

		c=getchar();

	}

	return w;

}

void insert(int x,int y,int z)

{

	l++;

	ver[l]=y;

	edge[l]=z;

	nxt[l]=head[x];

	head[x]=l;

}

void SPFA(int s)

{

	queue<int> q;

	memset(in,0,sizeof(in));

	memset(dis,0x3f,sizeof(dis));

	q.push(s);

	in[s]=1;

	dis[s]=0;

	while(!q.empty()){

		int x=q.front();

		q.pop();

		for(int i=head[x];i;i=nxt[i]){

			int y=ver[i];

			if(dis[y]>dis[x]+edge[i]){

				dis[y]=dis[x]+edge[i];

				if(!in[y]){

					q.push(y);

					in[y]=1;

				}

			}

		}

		in[x]=0;

	}

	for(int i=1;i<=k+1;i++) d[s][i]=dis[i];

	d[s][k+2]=dis[n];

}

signed main()

{

	freopen("atr.in","r",stdin);

	freopen("atr.out","w",stdout);

	n=read();m=read();k=read();

	for(i=1;i<=m;i++){

		int u,v,w;

		u=read();v=read();w=read();

		insert(u,v,w);

		insert(v,u,w);

	}

	c=read();

	for(i=1;i<=c;i++){

		int x,y;

		x=read();y=read();

		g[y]|=(1<<(x-2));

	}

	for(i=1;i<=k+1;i++) SPFA(i);

	memset(f,-1,sizeof(f));

	f[0][1]=0;

	for(i=0;i<=(1<<k)-1;i++){

		for(j=1;j<=k+1;j++){

		    if(f[i][j]!=-1){

				for(l=2;l<=k+1;l++){

					if((i&g[l])==g[l]){

						if(f[i|(1<<(l-2))][l]==-1) f[i|(1<<(l-2))][l]=f[i][j]+d[j][l];

						else f[i|(1<<(l-2))][l]=min(f[i|(1<<(l-2))][l],f[i][j]+d[j][l]);

					}

				}

			}

		}

	}

	int ans=1<<30;

	for(i=1;i<=k+1;i++){

		if(f[(1<<k)-1][i]!=-1) ans=min(ans,f[(1<<k)-1][i]+d[i][k+2]);

	}

	cout<<ans<<endl;

	fclose(stdin);

	fclose(stdout);

	return 0;

}