【转】海量数据解决思路之BitMap

转载（http://zengzhaozheng.blog.51cto.com/8219051/1404108）

一、概述

本文将讲述Bit-Map算法的相关原理,Bit-Map算法的一些利用场景，例如BitMap解决海量数据寻找重复、判断个别元素是否在海量数据当中等问题.最后说说BitMap的特点已经在各个场景的使用性。

二、Bit-Map算法

先看看这样的一个场景：给一台普通PC，2G内存，要求处理一个包含40亿个不重复并且没有排过序的无符号的int整数，给出一个整数，问如果快速地判断这个整数是否在文件40亿个数据当中？

问题思考：

40亿个int占（40亿*4）/1024/1024/1024 大概为14.9G左右，很明显内存只有2G，放不下，因此不可能将这40亿数据放到内存中计算。要快速的解决这个问题最好的方案就是将数据搁内存了，所以现在的问题就在如何在2G内存空间以内存储着40亿整数。一个int整数在java中是占4个字节的即要32bit位，如果能够用一个bit位来标识一个int整数那么存储空间将大大减少，算一下40亿个int需要的内存空间为40亿/8/1024/1024大概为476.83 mb，这样的话我们完全可以将这40亿个int数放到内存中进行处理。

具体思路：

1个int占4字节即4*8=32位，那么我们只需要申请一个int数组长度为 int tmp[1+N/32]即可存储完这些数据，其中N代表要进行查找的总数，tmp中的每个元素在内存在占32位可以对应表示十进制数0~31,所以可得到BitMap表:

tmp[0]:可表示0~31

tmp[1]:可表示32~63

tmp[2]可表示64~95

.......

那么接下来就看看十进制数如何转换为对应的bit位：

假设这40亿int数据为：6,3,8,32,36,......，那么具体的BitMap表示为：

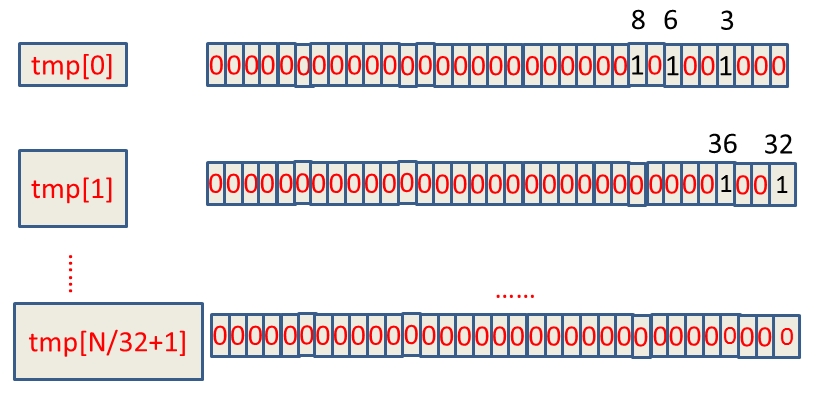
如何判断int数字在tmp数组的哪个下标，这个其实可以通过直接除以32取整数部分，例如：整数8除以32取整等于0，那么8就在tmp[0]上。另外，我们如何知道了8在tmp[0]中的32个位中的哪个位，这种情况直接mod上32就ok，又如整数8，在tmp[0]中的第8 mod上32等于8，那么整数8就在tmp[0]中的第八个bit位（从右边数起）。

三、Bit-Map算法原始实现

标注下，这部分来自blog：http://blog.csdn.net/hguisu/article/details/7880288的第五部分。好，来看看c语言的实现：

//set 设置所在的bit位为1
void set(int i) {
    a[i>>SHIFT] |=  (<<(i & MASK));
}
//clr 初始化所有的bit位为0
void clr(int i) {
    a[i>>SHIFT] &= ~(<<(i & MASK));
}
//test 测试所在的bit为是否为1
int  test(int i){
    return a[i>>SHIFT] &   (<<(i & MASK));
}
int main()
{   int i;
    for (i = ; i < N; i++)
        clr(i);
    while (scanf("%d", &i) != EOF)
        set(i);
    for (i = ; i < N; i++)
        if (test(i))
            printf("%d\n", i);
    return ;
}

注明： 左移n位就是乘以2的n次方，右移n位就是除以2的n次方

解析本例中的void set(int i) {        a[i>>SHIFT] |=  (1<<(i & MASK)); }
1)  i>>SHIFT： 
其中SHIFT=5，即i右移5为，2^5=32,相当于i/32，即求出十进制i对应在数组a中的下标。比如i=20，通过i>>SHIFT=20>>5=0 可求得i=20的下标为0；

2)  i & MASK： 
其中MASK=0X1F,十六进制转化为十进制为31，二进制为0001 1111，i&（0001 1111）相当于保留i的后5位。

比如i=23，二进制为：0001 0111，那么 
                        0001 0111 
                  &    0001 1111 = 0001 0111 十进制为：23 
比如i=83，二进制为：0000 0000 0101 0011，那么 
                         0000 0000 0101 0011 
                    &   0000 0000 0001 0000 = 0000 0000 0001 0011 十进制为：19

i & MASK相当于i%32。

3) 1<<(i & MASK) 
相当于把1左移 (i & MASK)位。 
比如(i & MASK)=20，那么i<<20就相当于： 
        0000 0000 0000 0000 0000 0000 0000 0001 << 20 
      =0000 0000 0001 0000 0000 0000 0000 0000

注意上面 “|=”.

在博文：位运算符及其应用 提到过这样位运算应用：

将int型变量a的第k位清0，即a=a&~(1<<k)
将int型变量a的第k位置1， 即a=a|(1<<k)

这里的将  a[i/32] |= (1<<M));第M位置1 .

4) void set(int i) {        a[i>>SHIFT]  |=  (1<<(i & MASK)); }等价于：

1. void set(int i)

2. {

3. a[i/32] |= (1<<(i%32));

4. }

即实现上面提到的三步：

1.求十进制0-N对应在数组a中的下标： n/32

2.求0-N对应0-31中的数：N%32=M

3.利用移位0-31使得对应32bit位为1: 1<<M，并置1;

四、BitMap算法一些其他应用场景扩展

(1)BitMap小小变种:2-BitMap。

看个小场景：在3亿个整数中找出不重复的整数，限制内存不足以容纳3亿个整数。

对于这种场景我可以采用2-BitMap来解决，即为每个整数分配2bit，用不同的0、1组合来标识特殊意思，如00表示此整数没有出现过，01表示出现一次，11表示出现过多次，就可以找出重复的整数了，其需要的内存空间是正常BitMap的2倍，为：3亿*2/8/1024/1024=71.5MB。

具体的过程如下：

扫描着3亿个整数，组BitMap，先查看BitMap中的对应位置，如果00则变成01，是01则变成11，是11则保持不变，当将3亿个整数扫描完之后也就是说整个BitMap已经组装完毕。最后查看BitMap将对应位为11的整数输出即可。

(2)对没有重复元素的整数进行排序。

对于非重复的整数排序BitMap有着天然的优势，它只需要将给出的无重复整数扫描完毕，组装成为BitMap之后，那么直接遍历一遍Bit区域就可以达到排序效果了。

举个例子：对整数4、3、1、7、6进行排序

BitMap如下：

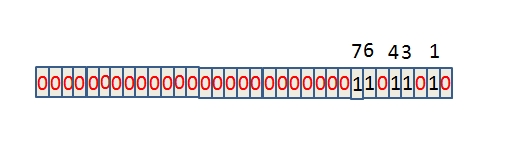
直接按Bit位输出就可以得到排序结果了。

五、总结

本文主要讲述了BitMap算法的相关概念以及其一些相关的应用场景和实现方法。其实BitMap的应用场景远远不止点，比如还可以用于压缩、爬虫系统中url去重、解决全组合问题。可能有些人觉得BitMap算法实现起来有点麻烦，其实某些语言是对BitMap算法进行了封装的，比如java中对应BitMap的数据结构就有BitSet类。其使用方法相当简单，看看API就ok,还是给个例子吧：

import java.util.BitSet;
public class Test{
    public static void main(String[] args) {
        int [] array = new int [] {1,2,3,22,0,3};
        BitSet bitSet  = new BitSet(6);
        //将数组内容组bitmap
        for(int i=0;i<array.length;i++)
        {
            bitSet.set(array[i], true);
        }
       System.out.println(bitSet.size());
        System.out.println(bitSet.get(3));
    }
}

对应的bit位如果有对应整数那么通过bitSet.get(x)会返回true，反之false。其中x为BitMap位置下标。

好了，BitMap就说到这里。下次blog说说处理海量数据的“万金油”-Hash算法,以及它在MapReduce框架中的应用。

参考文献：

http://blog.csdn.net/v_july_v/article/details/6685962

文章第三部分来自于：http://blog.csdn.net/hguisu/article/details/7880288