洛谷P1310 表达式的值——题解

题目传送

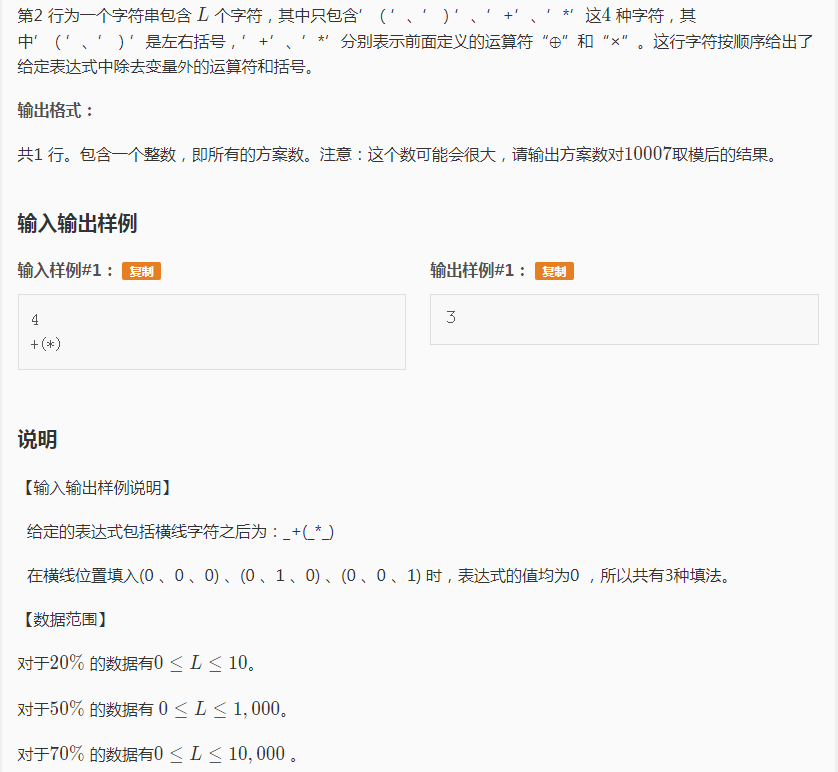
题的难点：1、有运算优先级，不好判断。2、有破坏整体和谐性的讨厌的括号。3、不知道哪里要填数。4、要求方案数很大，搜索不会做呐。

发现难点1和2都是中缀表达式的缺点。转成后缀表达式后难点1、2就烟消云散了。

普及一下：

　　前缀表达式（又称波兰表达式）与后缀表达式（又称逆波兰表达式）较我们平常使用的中缀表达式，最主要的特点是没有括号。前/后缀表达式是一种十分有用的表达式，将中缀表达式转换为前缀表达式后，就可以只依靠出栈、入栈两种简单操作完全解决中缀表达式的全部运算。而平常我们一般都用后缀表达式（顺序从前到后，而前缀表达式的扫描顺序是从后向前）。

　　计算后缀表达式，只要我们从前到后扫描，遇到数就入栈，遇到运算符就出栈两个数进行相应运算，最终弄结果再入栈。

　　这里给出一个中缀表达式转后缀表达式的方法（建树什么的就别提了）：

　　设用一个结果栈和一个符号栈。从前向后扫描中缀表达式：

　　1、若遇到数，直接入结果栈；

　　2、若遇到运算符，弹出符号栈栈顶连续的优先级高于它的运算符，让那些运算符按弹出顺序依次入结果栈后再自己入符号栈；

　　3、若遇到左括号，直接入符号栈；

　　4、若遇到右括号，一直弹出符号栈至第一次弹出左括号，将弹出的运算符（不包括括号）按弹出顺序依次入结果栈；

　　5、若扫描完中缀表达式后符号栈栈非空，则将符号栈元素全部弹出，将弹出的运算符按弹出顺序依次入结果栈。

　　最后结果栈存的就是转换完的后缀表达式。计算时只要从结果栈的栈底开始扫，按照后缀表达式的计算过程计算即可。

再考虑从哪里填数。发现当我们无视括号时，剩下运算符的前后都会有一个数、相邻两运算符间也会有一个数。加上括号后只会改变运算顺序，不会改变数的数量。考虑起始时在结果栈先入一个数，每次遇到加号或乘号后再入一个数。辩证正确性：如果该加号（或乘号）后面有括号时：若为左括号，由于左括号直接入符号栈，所以入左括号进符号栈和入数进结果栈这两步操作的顺序无关紧要；若为右括号，那么该运算符后面就应该有一个数。如果该加号（或乘号）后面没有括号时，后面就该有一个数。辩证结束。

由于题目中要求的是最终表达式值为0的方案数，发现可由每次运算结果为0的方案数和结果为1的方案数推出： 设某运算符左边为1的方案数有l1种、为零的方案数有l0种；右边为1的方案数有r1种，右边为0的方案数有r0种。若该运算符为+，则结果为1的方案数则有l1*r1+l0*r1+l1*r2种，结果为0的方案数则有l0*r0种；若该运算符为*，则结果为1的方案数则有l1*r1种，结果为0的方案数则有l1*r0+l0*r0+l0*r1种。由此可以增设两个栈zero、one，分别维护随着结果栈进行运算时运算符左右两边为0的方案数和为1的方案数。思路就到此为止了。

见AC代码：

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<stack>
 
 using namespace std;
 
 int lenl;
 
 const int mod=;
 
 char exp[];//一开始输入的中缀表达式 
 
 string pol="n";//用'n'代替要填的数。pol为结果栈，但发现用string更好维护，于是就换成了string型。 
 
 stack<char> sta;//符号栈 
 
 stack<int>zero,one,ope;//zero、one的意义见上文，ope为计算后缀表达式时用到的辅助栈 
 
 int main()
 {
     cin>>lenl;
     scanf("%s",exp);
     for(int k=;k<lenl;k++)//中缀表达式转后缀表达式
     {
         if(exp[k]=='*'||exp[k]=='(')
         sta.push(exp[k]);
         if(exp[k]=='+')
         {
             while(!sta.empty()&&sta.top()=='*')
             {
                 pol+='*';
                 sta.pop();
             }
             sta.push('+');
         }
         if(exp[k]==')')
         {
             while(sta.top()!='(')
             {
                 pol+=sta.top();
                 sta.pop();
             }
             sta.pop();
         }
         if(exp[k]=='*'||exp[k]=='+') pol+='n';//填数
     }
     while(!sta.empty())//别忘了把符号栈剩余的元素转到结果里
     {
         pol+=sta.top();
         sta.pop();
     }
     int l0,r0,l1,r1;
     for(int k=;k<pol.length();k++)//计算后缀表达式
     {
         if(pol[k]=='n')
         {
             zero.push();
             one.push();
         }
         if(pol[k]=='+')
         {
             l0=zero.top();zero.pop();
             l1=one.top();one.top();
             r0=zero.top();zero.pop();
             r1=one.top();one.top();
             zero.push(l0*r0%mod);
             one.push(((l0*r1+l1*r0)%mod+l1*r1)%mod);
         }
         if(pol[k]=='*')
         {
             l0=zero.top();zero.pop();
             l1=one.top();one.top();
             r0=zero.top();zero.pop();
             r1=one.top();one.top();
             zero.push(((l0*r0+l1*r0)%mod+l0*r1)%mod);
             one.push(l1*r1%mod);
         }
     }
     cout<<zero.top();//最终使表达式值为零的方案数
     return ;
 }

做这个题时如果不会转中缀表达式转后缀表达式的话模拟也是可以骗点分的，但要注意考虑周全。（就算是一点微不足道的手误，也能造就90分到10分的神话（说多了都是泪））