算法学习笔记【5】| ST表

ST表

Part 1:ST表解决的问题是什么

ST 表可以用来解决RMQ（区间最值问题）等可重复贡献的问题。

ST表基于倍增的思想来实现。

Part 2:ST表的实现

ST表通过 O(nlog⁡n)<script type="math/tex;mode=inline" id="MathJax-Element-4">O(n \log n)</script>O(n \log n) 的预处理，得到 O(1)<script type="math/tex;mode=inline" id="MathJax-Element-2">O(1)</script>O(1) 的询问。

定义：

• f[i][k] 表示 i 到 i+2k−1<script type="math/tex;mode=inline" id="MathJax-Element-3">i+2^k-1</script>i+2^k-1 中要维护的值（max，min，gcd等）。

初始化：

• f[i][0] = a[i]。

计算过程（以求 max 为例）：

for(int k=1;(1<<k)<=n;k++){
    for(int i=1;i+(1<<k)-1<=n;i++){
        f[i][k] = max(f[i][k-1],f[i+(1<<(k-1))][k-1]);
    }
}

这里使用了位运算来加速。

计算好了还需要支持查询，对此可以单独写一个函数：

int query(int l,int r){
    int k = log2(r-l+1);
    return max(f[l][k],f[r-(1<<k)+1][r]);
}

我们想要的是 l+2k−1≤r<script type="math/tex;mode=inline" id="MathJax-Element-5">l+2^k-1\le r</script>l+2^k-1\le r ，所以 k 就是 log2⁡(r−l+1)<script type="math/tex;mode=inline" id="MathJax-Element-1">\log_2(r-l+1)</script>\log_2(r-l+1) 。
下面的式子实际上表示了下图的样子：

<img src="https://pic3.zhimg.com/v2-595bdb6722409f9dc932362bb99ea4f6_b.jpg" data-caption="" data-size="normal" data-rawwidth="347" data-rawheight="106" class="content_image" width="347"/>

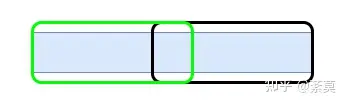
其中重叠的部分就解释了“可重复贡献”这个名词。

因为最大值始终是最大值，我只需要覆盖整个区间即可，而不需要精准覆盖。

Part 3:例题和代码

例题

注意这题有点卡时间，最好优化一下计算 log2 的部分和输入输出。

const int N=100005;
int n,m,a[N],f[N][20],lg2[N];
void init(){
    for(int k=1;(1<<k)<=n;k++){
        for(int i=1;i+(1<<k)-1<=n;i++){
            f[i][k] = max(f[i][k-1],f[i+(1<<(k-1))][k-1]);
        }
    }
}
int query(int l,int r){
    int k = lg2[r-l+1];
    return max(f[l][k],f[r-(1<<k)+1][k]);
}
int main(){
    n=read();m=read();
    F(i,2,n) lg2[i] = lg2[i/2] + 1;
    F(i,1,n) f[i][0] = read();
    init();
    while(m--){
        int l=read(),r=read();
        writeln(query(l,r));
    }
    return 0;
}