2D KD-Tree实现

KD-tree

1.使用背景

在项目中遇到一个问题: 如何算一个点到一段折线的最近距离~折线的折点可能有上千个, 而需要检索的点可能出现上万的数据量, 的确是个值得思考的问题~

2.暴力解法

有个比较直观的方法: 计算点到折线的每段的距离, 然后暴力找出最短的那段~得到解..不过这种O(n)的复杂度方法显然遇到大数据量的时候会严重拖累服务器的性能.

3.K临近算法-数据结构

knn给了一个非常巧妙的启示用于求近似解, 可以通过2D-tree(k=2)得到.
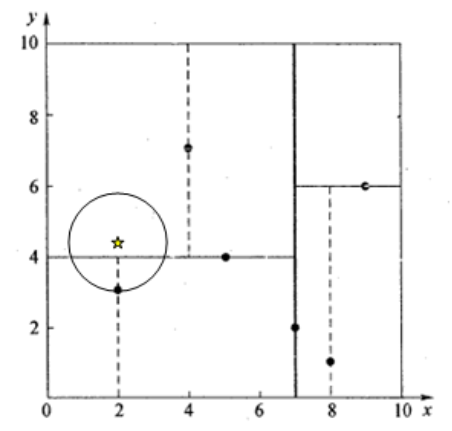
举一个稍微复杂的例子，我们来查找点(2,4.5)，在(7,2)处测试到达(5,4)，在(5,4)处测试到达(4,7)，然后search_path中的结点为<(7,2), (5,4), (4,7)>，从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202；
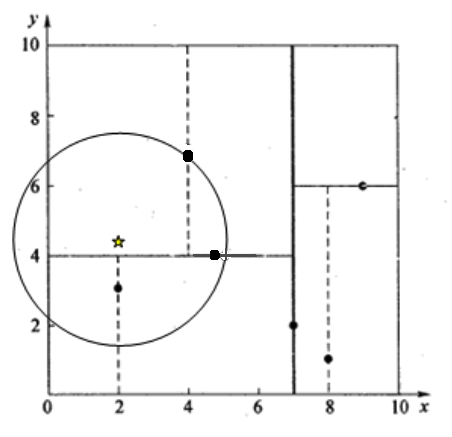
然后回溯至(5,4)，以(2,4.5)为圆心，以dist=3.202为半径画一个圆与超平面y=4相交，如下图，所以需要跳到(5,4)的左子空间去搜索。所以要将(2,3)加入到search_path中，现在search_path中的结点为<(7,2), (2, 3)>；另外，(5,4)与(2,4.5)的距离为3.04 < dist = 3.202，所以将(5,4)赋给nearest，并且dist=3.04。
回溯至(2,3)，(2,3)是叶子节点，直接平判断(2,3)是否离(2,4.5)更近，计算得到距离为1.5，所以nearest更新为(2,3)，dist更新为(1.5)
回溯至(7,2)，同理，以(2,4.5)为圆心，以dist=1.5为半径画一个圆并不和超平面x=7相交, 所以不用跳到结点(7,2)的右子空间去搜索。
至此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2,4.5)的最近邻点，最近距离为1.5。

4.代码实现

KDTree.h

#define lson (rt << 1)//左节点
#define rson (rt << 1 | 1)//右节点

#include <vector>
#include <algorithm>
#include <cmath>

    const int N = 50005;
    const int k = 2; //2D-tree

    struct Node {
        float feature[2];//feature[0] = x, feature[1] = y
        static int idx;
        Node(float x0, float y0) {
            feature[0] = x0;
            feature[1] = y0;
        }
        bool operator < (const Node &u) const {
            return feature[idx] < u.feature[idx];
        }
        //TOOD =hao
        Node() {
            feature[0] = 0;
            feature[0] = 0;
        }
    };

    class KDTree {
    public:
        KDTree();
        ~KDTree();
        void clean();
        int read_in(float* ary_x, float* ary_y, int len);
        void build(int l, int r, int rt, int dept);
        int find_nearest_point(float x, float y, Node& result, float& dist);
        float distance(const Node& x, const Node& y);
    private:
        void query(const Node& p, Node& res, float& dist, int rt, int dept);
        std::vector<Node> _data;//用vector模拟数组
        std::vector<int> _flag;//判断是否存在
        int _idx;
        std::vector<Node> _find_nth;
    };

KD-tree.cpp

    #include "KDTree.h"
    int Node::idx = 0;
    KDTree::KDTree() {
        _data.reserve(N * 4);
        _flag.reserve(N * 4);//TODO init
    }

    KDTree::~KDTree() {}

    int KDTree::read_in(float* ary_x, float* ary_y, int len) {
        _find_nth.reserve(N * 4);
        for (int i = 0; i < len; ++i) {
            Node tmp(ary_x[i], ary_y[i]);
            _find_nth.push_back(Node(ary_x[i], ary_y[i]));
        }
        for (int i = 0; i < N * 4; ++i) {
            Node tmp;
            _data.push_back(tmp);
            _flag.push_back(0);
        }
        build(0, len - 1, 1, 0);
        return 0;
    }

    void KDTree::clean() {
        _find_nth.clear();
        _data.clear();
        _flag.clear();
    }

    //建立kd-tree
    void KDTree::build(int l, int r, int rt, int dept) {
        if (l > r) return;
        _flag[rt] = 1;                  //表示标号为rt的节点存在
        _flag[lson] = _flag[rson] = -1; //当前节点的孩子暂时标记不存在
        int mid = (l + r + 1) >> 1;
        Node::idx = dept % k;           //按照编号为idx的属性进行划分
        std::nth_element(_find_nth.begin() + l, _find_nth.begin() + mid, _find_nth.begin() + r + 1);
        _data[rt] = _find_nth[mid];
        build(l, mid - 1, lson, dept + 1); //递归左子树
        build(mid + 1, r, rson, dept + 1);
    }

    int KDTree::find_nearest_point(float x, float y, Node &res, float& dist) {
        Node p(x, y);
        query(p, res, dist, 1, 0);
        return 0;
    }

    //查找kd-tree距离p最近的点
    void KDTree::query(const Node& p, Node& res, float& dist, int rt, int dept) {
        if (_flag[rt] == -1) {
            return;
        }//不存在的节点不遍历
        float tmp_dist = distance(_data[rt], p);
        bool fg = false; //用于标记是否需要遍历右子树
        int dim = dept % k; //和建树一样, 保证相同节点的dim值不变
        int x = lson;
        int y = rson;
        if (p.feature[dim] >= _data[rt].feature[dim]) {
            std::swap(x, y);  //数据p的第dim个特征值大于等于当前的数据，则需要进入右子树
        }
        if (~_flag[x]) {
            query(p, res, dist, x, dept + 1); //节点x存在, 则进入子树继续遍历
        }

        if (tmp_dist < dist) { //如果找到更小的距离, 则替换目前的结果dist
            res = _data[rt];
            dist = tmp_dist;
        }
        tmp_dist = (p.feature[dim] - _data[rt].feature[dim]) * (p.feature[dim] - _data[rt].feature[dim]);
        if (tmp_dist < dist) { //还需要继续回溯
            fg = true;
        }
        if (~_flag[y] && fg) {
            query(p, res, dist, y, dept + 1);
        }
    }

    //计算两点间的距离的平方
    float KDTree::distance(const Node& x, const Node& y) {
        float res = 0;
        for (int i = 0; i < k; i++) {
            res += (x.feature[i] - y.feature[i]) * (x.feature[i] - y.feature[i]);
        }
        return res;
    }

自测暂无发现bug~
参考文章:
(http://blog.csdn.net/acdreamers/article/details/44664645/ “KD-tree实现”)
(http://blog.csdn.net/silangquan/article/details/41483689/ “详解KD-tree”)
感谢巨巨们的分享