numpy基础--线性代数

以下代码的前提：import numpy as np

线性代数（如矩阵乘法、矩阵分解、行列式以及其他方阵数学等）是任何数组库的重要组成部分。numpy提供了一个用于矩阵乘法的dot函数（既是一个数组方法也是numpy命名空间中的一个函数）。

矩阵乘法官方说明：numpy.dot — NumPy v1.21 Manual

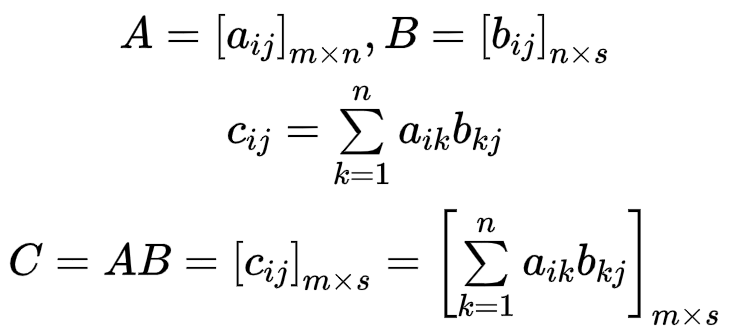
 1 >>> x = np.array([[1, 2, 3], [4, 5, 6]])
 2 >>> y = np.array([[1, 2], [3, 4], [5, 6]])
 3 >>> x
 4 array([[1, 2, 3],
 5        [4, 5, 6]])
 6 >>> y
 7 array([[1, 2],
 8        [3, 4],
 9        [5, 6]])
10 >>> np.dot(x, y)
11 array([[22, 28],
12        [49, 64]])
13 >>> x.dot(y)
14 array([[22, 28],
15        [49, 64]])
16 >>>

numpy.linalg中有一组标准的矩阵分解运算以及诸如求逆和行列式之类的东西。

 1 >>> from numpy.linalg import inv, qr
 2 >>> X = np.arange(9).reshape(3, 3)
 3 >>> X
 4 array([[0, 1, 2],
 5        [3, 4, 5],
 6        [6, 7, 8]])
 7 >>> mat = X.T.dot(X)
 8 >>> mat
 9 array([[45, 54, 63],
10        [54, 66, 78],
11        [63, 78, 93]])
12 >>> inv(mat)
13 array([[ 3.51843721e+13, -7.03687442e+13,  3.51843721e+13],
14        [-7.03687442e+13,  1.40737488e+14, -7.03687442e+13],
15        [ 3.51843721e+13, -7.03687442e+13,  3.51843721e+13]])
16 >>> mat.dot(inv(mat))
17 array([[ 0.79296875,  1.        , -0.2109375 ],
18        [ 0.1484375 ,  1.        , -0.046875  ],
19        [-0.74609375,  1.        ,  0.6171875 ]])
20 >>> q, r = qr(mat)
21 >>> q
22 array([[-0.47673129,  0.77849894,  0.40824829],
23        [-0.57207755,  0.07784989, -0.81649658],
24        [-0.66742381, -0.62279916,  0.40824829]])
25 >>> r
26 array([[-9.43927963e+01, -1.15559666e+02, -1.36726535e+02],
27        [ 0.00000000e+00, -1.40129810e+00, -2.80259620e+00],
28        [ 0.00000000e+00,  0.00000000e+00,  3.55271368e-15]])
29 >>>

下表是常用的numpy.linalg函数。

方法	说明
diag	以一维数组的形式返回方阵的对角线（或非对角线）元素，或将一维数组转换为方阵（非对角线元素为0）
dot	矩阵乘法
trace	计算对角线元素的和
det	计算矩阵行列式
eig	计算方阵的本征值和本征向量
inv	计算方阵的逆
solve	解线性方程组Ax=b，其中A为一个方阵
lstsq	计算Ax=b的最小二乘解

numpy.diag — NumPy v1.21 Manual

numpy.diag(v, k=0)：取矩阵主对角线的值，k=0，取主对角线；k>0，取主对角线之上；k<0，取主对角线之下。

>>> x = np.arange(9).reshape(3, 3)
>>> x
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])
>>> np.diag(x)
array([0, 4, 8])
>>> np.diag(x, k=1)
array([1, 5])
>>> np.diag(x, k=-1)
array([3, 7])
>>> np.diag(np.diag(x))
array([[0, 0, 0],
       [0, 4, 0],
       [0, 0, 8]])

numpy.trace — NumPy v1.21 Manual

矩阵的迹：矩阵主对角线元素之和。

>>> x = np.eye(3)
>>> x
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
>>> x.trace()
3.0

numpy.linalg.det — NumPy v1.21 Manual

矩阵（必须是方阵）行列式的值：The determinant of a 2-D array [[a, b], [c, d]] is ad - bc:

>>> a = np.array([[1, 2], [3, 4]])
>>> a
array([[1, 2],
       [3, 4]])
>>> np.linalg.det(a)
-2.0000000000000004

numpy.linalg.eig — NumPy v1.21 Manual

方阵的本征值和本征向量：

>>> from numpy import linalg as LA
>>> x = np.diag((1, 2, 3))
>>> x
array([[1, 0, 0],
       [0, 2, 0],
       [0, 0, 3]])
>>> w, v = LA.eig(x)
>>> w; v
array([1., 2., 3.])
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])

numpy.linalg.inv — NumPy v1.21 Manual

矩阵的逆：设A是一个n阶矩阵，若存在另一个n阶矩阵B，使得：AB=BA=E ，则称方阵A可逆，并称方阵B是A的逆矩阵。

>>> from numpy.linalg import inv
>>> a = np.array([[1., 2.], [3., 4.]])
>>> a
array([[1., 2.],
       [3., 4.]])
>>> ainv = inv(a)
>>> ainv
array([[-2. ,  1. ],
       [ 1.5, -0.5]])

numpy.linalg.solve — NumPy v1.21 Manual

解线性方程组Ax=b，其中A为一个方阵。

>>> a = np.array([[1, 2], [3, 5]])
>>> b = np.array([1, 2])
>>> x = np.linalg.solve(a, b)
>>> x
array([-1.,  1.])