题解 CF1292A

题目大意：

给你 \(2\times n\) 的迷宫，初始时没有任何障碍，给定 \(q\) 次询问，每次询问给予坐标 \((x,y)\)，问将坐标 \((x,y)\) 反转状态（即无障碍变有障碍，有障碍变无障碍）后，该迷宫还能否到达终点 \((2,n)\)，并应用更改。

题目分析：

因为是 \(2\times n\) 的迷宫，很显然的是，若下方一个位置为有障碍，则他的左上角或正上方或右上角有障碍时，角色无法到达终点。

同理，对于上方的情况，就是他的左下角或正下方或右下角有障碍时，角色无法到达终点。

如果觉得不大显然的话，可以看下图：

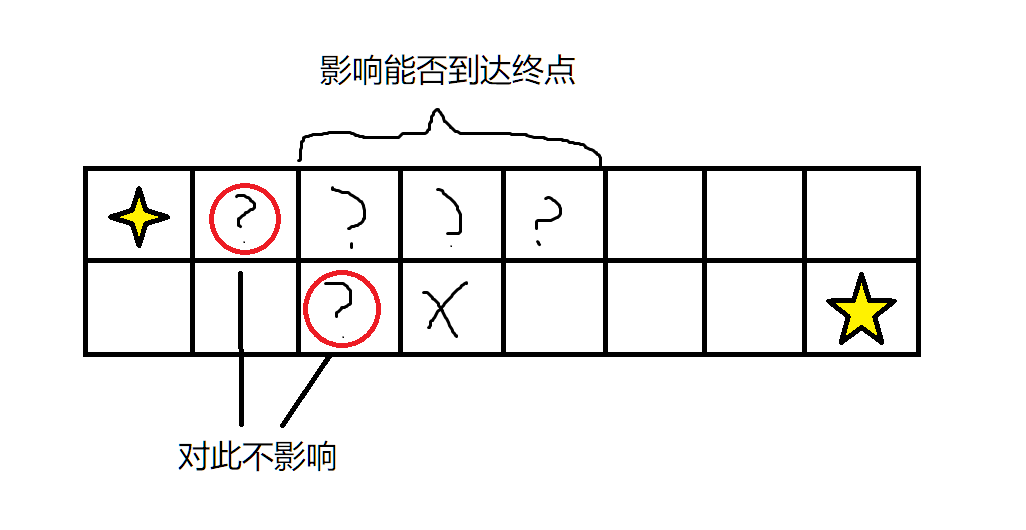
故，我们只需要统计一下形成关联的地方有多少就行了，时间复杂度 \(O(q)\)。

代码实现：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define TIME_LIMIT (time_t)1.5e3
#define dbg(x) cerr<<#x<<": "<<x<<endl;
#define MAX_SIZE (int)114514
bool bmap[2][MAX_SIZE];
signed main() {
    ios::sync_with_stdio(false);
#ifdef LOCAL
    freopen("in.in", "r", stdin);
    freopen("out.out", "w", stdout);
    time_t cs = clock();
#endif
    //========================================
    int n, q;
    cin >> n >> q;
    int blocked = 0;

    while (q--) {
        int x, y;
        cin >> x >> y;
        x -= 1;

        if (x) {
            if (bmap[x][y]) {
                blocked -= bmap[x - 1][y - 1];
                blocked -= bmap[x - 1][y];
                blocked -= bmap[x - 1][y + 1];
            } else {
                blocked += bmap[x - 1][y - 1];
                blocked += bmap[x - 1][y];
                blocked += bmap[x - 1][y + 1];
            }
        } else {
            if (bmap[x][y]) {
                blocked -= bmap[x + 1][y - 1];
                blocked -= bmap[x + 1][y];
                blocked -= bmap[x + 1][y + 1];
            } else {
                blocked += bmap[x + 1][y - 1];
                blocked += bmap[x + 1][y];
                blocked += bmap[x + 1][y + 1];
            }
        }

        bmap[x][y] = !bmap[x][y];

        if (blocked)
            cout << "No" << endl;
        else
            cout << "Yes" << endl;
    }

    //========================================
#ifdef LOCAL
    fclose(stdin);
    fclose(stdout);
    time_t ce = clock();
    cerr << "Used Time: " << ce - cs << " ms." << endl;

    if (TIME_LIMIT < ce - cs)
        cerr << "Warning!! Time exceeded limit!!" << endl;

#endif
    return 0;
}