【题解】A18537.我心中珍藏的游戏

题目跳转

思路：

题目问最多可以获得的额外伤害，其实就是询问在这些技能中，如何怎样选取一个最优的发动技能顺序使得攻击加成最大。我们可以把每一个技能看作成一个图的顶点，把每一个攻击加成看作图的边，权制为\(Ei,j\)。由于\(Ei,j\)与\(Ej,i\)相等，则可以将这个图视为无向图。 可以样样例抽象成下图：

3
0 3 5
3 0 10
5 10 0

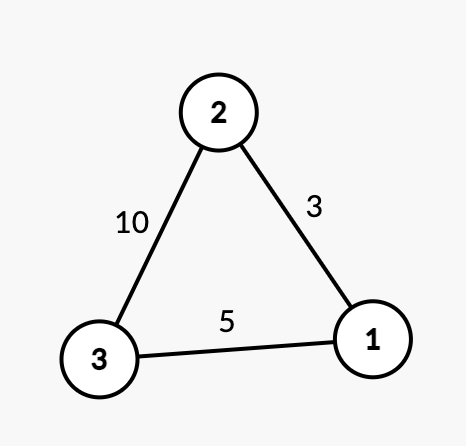
考虑使用贪心的思想来解决本题，每次在图中找到权值最大的一条边选择即可，但图中不能出现环。因为是无向图，在考虑的时候可以忽略技能使用的顺序。接下来就是找一个最大生成树即可。

时间复杂度分析：本道题可以使用最小生成树Kruskal算法来实现，将题目的模型抽象化后可以被看作为一个最多有\(\frac{(1+n)*n}{2} - n\)条边的无向图（化简后可得\(\frac{n^2 - n}{2}\))。注意一开始需要对每一条边进行排序。本道题的时间复杂度约为\(O(2\times n^2 \log_2{n})\)。

参考代码：

#include <iostream>
#include <algorithm>
using namespace std;

int n, cnt, ans;
int f[805];
struct edge{
    int x, y, z;
} edges[700005];

bool cmp(edge a, edge b){
    return a.z > b.z;
}

int getf(int x){
    if (f[x] == x) return x;
    return f[x] = getf(f[x]);
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    cin >> n;
    for (int i=1; i<=n; i++){
        f[i] = i;
        for (int j=1; j<=n; j++){
            int t; cin >> t;
            if (i == j || t == 0) continue;
            edges[++cnt] = (edge){i, j, t};
        }
    }
    sort(edges+1, edges+1+cnt, cmp);
    for (int i=1; i<=cnt; i++){
        int u = edges[i].x;
        int v = edges[i].y;
        int U = getf(u), V = getf(v);
        if (U != V){
            f[U] = V;
            ans += edges[i].z;
        }
    }
    cout << ans << endl;
    return 0;
}