混沌数学之拉比诺维奇-法布里康特方程(Rabinovich-Fabrikant equations)
拉比诺维奇-法布里康特方程(Rabinovich-Fabrikant equations)是
1979年苏联物理学家拉比诺维奇和法布里康特提出模拟非平衡介
质自激波动的非线性常微分方程组:
dot{x} = y (z - 1 + x^2) + \gamma x
dot{y} = x (3z + 1 - x^2) + \gamma y
dot{z} = -2z (\alpha + xy)
其中 α, γ 是控制系统的参数.
Danca and Chen指出由于拉比诺维奇-法布里康特方程包含平方项,
因此比较难以分析,即便选择的参数相同,但由于求解微分方程
组的步骤的不同也会导致不同的吸引子。
参数值:α=1.1,γ=0.803..0.917,t=0...130
初始条件:x(0)=-1,y(0)=0,z(0)=0.5
在t<20时,系统表现为自激振动,当t>20,系统进入馄饨态。
相关软件:混沌数学及其软件模拟
相关代码:
class RabinovichFabrikantEquation : public DifferentialEquation
{
public:
RabinovichFabrikantEquation()
{
m_StartX = -1.0f;
m_StartY = 0.0f;
m_StartZ = 0.5f; m_ParamA = 1.1f;
m_ParamB = 0.87f; m_StepT = 0.002f;
} void Derivative(float x, float y, float z, float& dX, float& dY, float& dZ)
{
dX = y*(z - + x*x) + m_ParamB*x;
dY = x*(*z + - x*x) + m_ParamB*y;
dZ = -*z*(m_ParamA + x*y);
} bool IsValidParamA() const {return true;}
bool IsValidParamB() const {return true;}
};
相关截图:


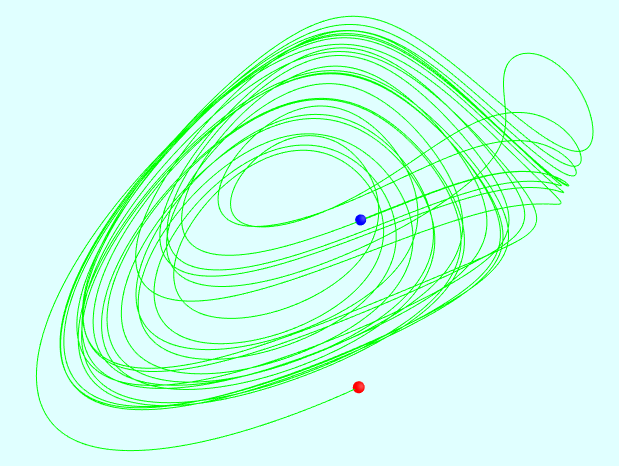

混沌数学之拉比诺维奇-法布里康特方程(Rabinovich-Fabrikant equations)的更多相关文章
- 混沌数学之Duffing(杜芬)振子
杜芬振子 Duffing oscillator是一个描写强迫振动的振动子,由非线性微分方程表示 杜芬方程列式如下: 其中 γ控制阻尼度 α控制韧度 β控制动力的非线性度 δ驱动力的振幅 ω驱动力的圆频 ...
- 混沌数学之Chua's circuit(蔡氏电路)
蔡氏电路(英语:Chua's circuit),一种简单的非线性电子电路设计,它可以表现出标准的混沌理论行为.在1983年,由蔡少棠教授发表,当时他正在日本早稻田大学担任访问学者[1].这个电路的制作 ...
- 混沌数学之Lorenz(洛伦茨)吸引子
洛伦茨吸引子是洛伦茨振子(Lorenz oscillator)的长期行为对应的分形结构,以爱德华·诺顿·洛伦茨的姓氏命名. 洛伦茨振子是能产生混沌流的三维动力系统,是一种吸引子,以其双纽线形状而著称. ...
- 混沌数学之logistic模型
logistic回归又称logistic回归分析,主要在流行病学中应用较多,比较常用的情形是探索某疾病的危险因素,根据危险因素预测某疾病发生的概率. 相关DEMO参见:混沌数学之离散点集图形DEMO ...
- 混沌数学之Henon吸引子
Henon吸引子是混沌与分形的著名例子. 相关软件:混沌数学及其软件模拟相关代码: // http://wenku.baidu.com/view/d51372a60029bd64783e2cc0.ht ...
- 混沌数学之Rössler(若斯叻)吸引子
若斯叻吸引子(Rössler attractor)是一组三元非线性微分方程: frac{dx(t)}{dt} = -y(t)-z(t) frac{dy(t)}{dt} = x(t)+a*y(t) fr ...
- 混沌数学之ASin模型
相关软件:混沌数学之离散点集图形DEMO 相关代码: class ASinEquation : public DiscreteEquation { public: ASinEquation() { m ...
- 混沌数学之Kent模型
相关软件:混沌数学之离散点集图形DEMO 相关代码: // http://wenku.baidu.com/view/7c6f4a000740be1e650e9a75.html // 肯特映射 clas ...
- 混沌数学之Feigenbaum模型
1975年,物理学家米切尔·费根鲍姆(Mitchell Feigenbaum)发现,一个可用实验加以测 量的特殊数与每个周期倍化级联相联系.这个数大约是4.669,它与π并列成为似乎在数学 ...
随机推荐
- 20169211《Linux内核原理与分析》 第十周作业
一.Linux内核之进程地址空间学习总结 Linux内核除了要管理物理内存还需要管理虚拟内存.用户进程的地址空间就是虚拟内存的一部分.每个用户进程都独有一个地址空间.由于是虚拟化的内存,所以从每个进程 ...
- ES6-const注意
注意要点 const 如何做到变量在声明初始化之后不允许改变的?其实 const 其实保证的不是变量的值不变,而是保证变量指向的内存地址所保存的数据不允许改动.此时,你可能已经想到,简单类型和复合类型 ...
- SpringMvc和servlet对比
一.servlet实现登录. 咱们先来看一下servlet实现注册登录. <servlet> <servlet-name>LoginServlet</servlet-na ...
- Servlet的基本架构
Servlet的基本架构: package test; import java.io.IOException; import javax.servlet.ServletException; impor ...
- QT学习笔记4:QT中GraphicsView编程
一.QGraphicsScene 1.QGraphicsScene QGraphicsScene继承自QObject,是一个管理图元的容器,与QGraphicsView合用可以在2D屏幕上显示如线.三 ...
- BZOJ3589动态树
**错误改了一上午. 先做熟练泼粪 k<=5,因此我们可以模拟这个过程,在线段树上把标记建出来然后pushup时候更新就好了. By:大奕哥 #include<bits/stdc++.h& ...
- [Agc001E] BBQ Hard
[Agc001E] BBQ Hard 题目大意 给定\(n\)对正整数\(a_i,b_i\),求\(\sum_{i=1}^{n-1} \sum_{j=i+1}^n \binom{a_i+b_i+a_j ...
- java多线程技术之条件变量
上一篇讲述了并发包下的Lock,Lock可以更好的解决线程同步问题,使之更面向对象,并且ReadWriteLock在处理同步时更强大,那么同样,线程间仅仅互斥是不够的,还需要通信,本篇的内容是基于上篇 ...
- Codeforces Round #351 (VK Cup 2016 Round 3, Div. 2 Edition) A. Bear and Game 水题
A. Bear and Game 题目连接: http://www.codeforces.com/contest/673/problem/A Description Bear Limak likes ...
- MYSQL分段统计
产品表 CREATE TABLE `product` ( `product_id` int(11) NOT NULL AUTO_INCREMENT, `product_model` varchar(2 ...
