洛谷 P2144 [FJOI2007]轮状病毒

P2144 [FJOI2007]轮状病毒

题目描述

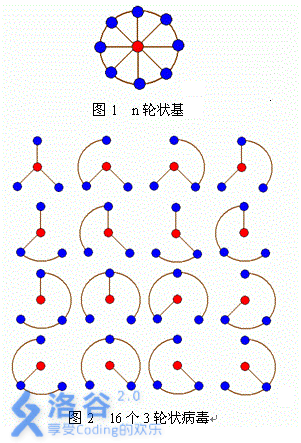
轮状病毒有很多变种。许多轮状病毒都是由一个轮状基产生。一个\(n\)轮状基由圆环上\(n\)个不同的基原子和圆心的一个核原子构成。\(2\)个原子之间的边表示这\(2\)个原子之间的信息通道，如图\(1\)。

\(n\)轮状病毒的产生规律是在\(n\)轮状基中删除若干边，使各原子之间有唯一一条信息通道。例如，共有\(16\)个不同的\(3\)轮状病毒，如图\(2\)所示。

给定\(n(n\le100)\)，编程计算有多少个不同的\(n\)轮状病毒。

输入输出格式

输入格式：

第一行有\(1\)个正整数\(n\)。

输出格式：

将编程计算出的不同的\(n\)轮状病毒数输出

---

发现题目要求求出看起来很有规律的无向图生成树个数，显然可以找一些规律/打表/递推之类的，但不妨采用比较暴力的方法，矩阵树定理。

然后发现事情并没有那么简单，如果用矩阵树定理暴力去做的话，你可以选择一些乱搞/手写高精度小数类之类的方法

而之前又说，这个图比较特殊，所以，我们可以研究一下基尔霍夫矩阵的行列式有没有什么比较特殊的求法，\(n+1(n>2)\)阶的基尔霍夫矩阵大概长这个样子

\[\begin{bmatrix}n&-1&-1&-1&-1&\cdots&-1&-1&-1\\-1&3&-1&0&0&\cdots&0&0&-1\\-1&-1&3&-1&0&\dots&0&0&0\\-1&0&-1&3&-1&\cdots&0&0&0\\\vdots&\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\-1&0&0&0&0&\cdots&-1&3&-1\\-1&-1&0&0&0&\cdots&0&-1&3\end{bmatrix}
\]

\(n\)阶主子式肯定是扔第一行第一列啊，因为我们想找行列式的递推规律，然后变成这样

\[\begin{bmatrix}3&-1&0&0&\cdots&0&0&-1\\-1&3&-1&0&\dots&0&0&0\\0&-1&3&-1&\cdots&0&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\0&0&0&0&\cdots&-1&3&-1\\-1&0&0&0&\cdots&0&-1&3\end{bmatrix}
\]

设这个矩阵为\(A_n\)，那么\(n\)的答案就是\(\det A_n\)，然后我们考虑求出这个矩阵的行列式

由“行列式等于它的任一行（列）的各元素与其对应的代数余子式乘积之和”

• 余子式：在\(n\)阶行列式中，把元素\(a_{i,j}\)所在第\(i\)行和第\(j\)行划去后，留下的\(n-1\)阶行列式叫元素\(a_{i,j}\)的余子式，记做\(M_{i,j}\)，定义代数余子式为\(A_{i,j}=(-1)^{i+j}M_{i,j}\)

我们可以扔第一行，因为\((1,n)\)和\((n,1)\)两个位置的东西看起来巨难受。

拆开第一行第一列得到

\[3\begin{vmatrix}3&-1&0&\dots&0&0&0\\-1&3&-1&\cdots&0&0&0\\\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\0&0&0&\cdots&-1&3&-1\\0&0&0&\cdots&0&-1&3\end{vmatrix}
\]

这个看起来就可以递推的东西，设\(n-1\)阶的它为\(B_{n-1}\)。为了方便，以下\(A_n,B_n\)也指代行列式的值。

然后剩下有贡献的第一行第二列和第一行第\(n-1\)列，因为余子式的正负与\(n\)有关，不妨先设\(n\)为奇数，偶数的情况是一样的。

\[\begin{vmatrix}-1&-1&0&\dots&0&0&0\\0&3&-1&\cdots&0&0&0\\\vdots&\vdots&\vdots&\ddots&\vdots&\vdots&\vdots\\0&0&0&\cdots&-1&3&-1\\-1&0&0&\cdots&0&-1&3\end{vmatrix}
\]

这是拆了第一行第二列，没思路再拆，发现扔第一行第一列后是\(-B_{n-2}\)，扔第\(n-1\)行第\(1\)列是主对角线全为\(-1\)的下三角，行列式的值为\(-1\)，再乘上\((-1)^{n-1+1}(-1)\)还是\(-1\)

然后是第一行第\(n\)列

\[-\begin{vmatrix}-1&3&-1&0&\dots&0&0\\0&-1&3&-1&\cdots&0&0\\\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\0&0&0&0&\cdots&-1&3\\-1&0&0&0&\cdots&0&-1\end{vmatrix}
\]

注意这里是负的，因为\(n\)是奇数。然后还是拆第一列，发现答案还是\(-B_{n-2}\)和\(-1\)

于是我们有\(A_n=3B_{n-1}-2B_{n-2}-2\)

以同样的方法对\(B\)做讨论，可以得到\(B_n=3B_{n-1}-B_{n-2}\)

然后联立一下得到\(A_{n}=3A_{n-1}-A_{n-2}+2\)，带入到\(n\le2\)发现式子仍然成立，然后直接递推+高精即可。

---

Code:

#include <cstdio>
#include <cstring>
const int N=110;
struct bignum
{
    int num[N];
    bignum(){memset(num,0,sizeof(num));}
    bignum friend operator +(bignum n1,bignum n2)
    {
        int len=n1.num[0]>n2.num[0]?n1.num[0]:n2.num[0];
        for(int i=1;i<=len;i++)
        {
            n1.num[i]+=n2.num[i];
            n1.num[i+1]+=n1.num[i]/10;
            n1.num[i]%=10;
        }
        if(n1.num[len+1]) n1.num[0]=len+1;
        else n1.num[0]=len;
        return n1;
    }
    bignum friend operator -(bignum n1,bignum n2)
    {
        int len=n1.num[0];
        for(int i=1;i<=len;i++)
        {
            n1.num[i]-=n2.num[i];
            if(n1.num[i]<0)
                n1.num[i]+=10,n1.num[i+1]--;
        }
        if(n1.num[len]) n1.num[0]=len;
        else n1.num[0]=len-1;
        return n1;
    }
}ans[N],two;
int main()
{
    int n;scanf("%d",&n);
    ans[1].num[0]=1,ans[1].num[1]=1,ans[2].num[0]=1,ans[2].num[1]=5,two.num[0]=1,two.num[1]=2;
    for(int i=3;i<=n;i++) ans[i]=ans[i-1]+ans[i-1]+ans[i-1]-ans[i-2]+two;
    for(int i=ans[n].num[0];i;i--) printf("%d",ans[n].num[i]);
    return 0;
}

---

2018.12.20