MT【145】不变的平面角

(2018,4月学考数学选择最后一题)
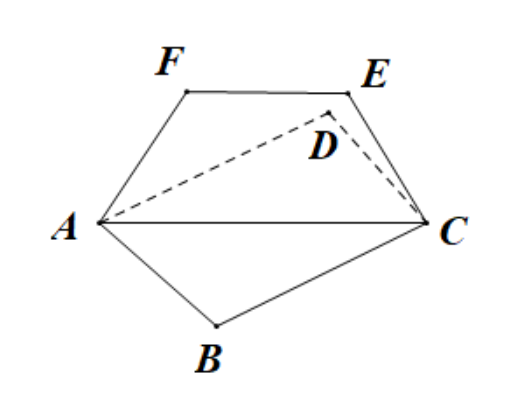
如图,设矩形$ABCD$所在平面与梯形$ACEF$所在平面相交于$AC$.

若$AB=1,BC=\sqrt{3},AF=EF=EC=1,$则下面二面角的平面角为定值的是( )
   A.F-AB-C           B.B-EF-D             C.A-BF-C              D.D- FA -B 

答案:B

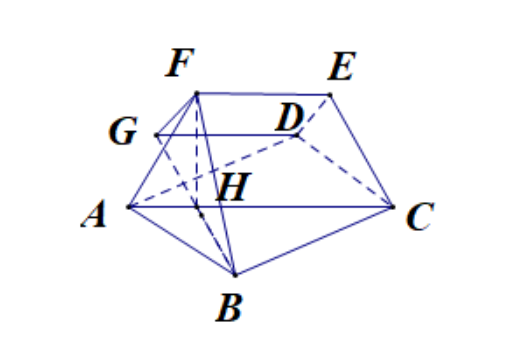
提示:事实上,如图我们只需作$FH\bot AC$,连接$BH,BF$则容易证明$BF\bot EF$,
同理$,ED\bot EF$,过$D$作$AC$的平行线,交$BH$的延长线于$G$,连接$GF$

故$B-EF-D$ 的平面角为$\angle BFG$. 变动过程中我们发现$F$是在以$BG$为直径的圆周上运动,故$\angle BFG=90^{o}$

                                                

注:如果看左视图，更能快速的获得答案.

练习:

如图,矩形$ABCD$中,$AB=1,BC=\sqrt{3}$,将$\Delta ABD$沿着$BD$向上翻折,若翻折过程中$AC$长度在$\left[\dfrac{\sqrt{10}}{2},\dfrac{\sqrt{13}}{2}\right]$内变化,则点$A$所形成的运动轨迹的长度为_____

答案：$\dfrac{\sqrt{3}\pi}{12}$