单自由度系统中质量、阻尼和刚度变化对频率响应函数(FRF)影响图的绘制

作者：赵兵

日期：2020-02-17

---

目录

单自由度系统中质量、阻尼和刚度变化对频率响应函数(FRF)影响图的绘制

1.     背景

2.     VISIO绘制

3.     Matlab绘制

　　(1)     M变化时

　　(2)     K变化时

　　(3)     C变化时

4.     参考文章

---

1. 背景

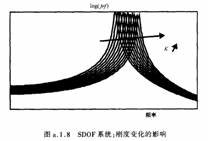
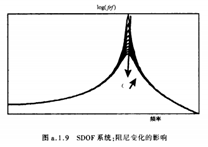
写文章时需要用到几张图,下面是从PDF上截图截出来的，用来表示单自由度系统在冲击激励下的频率响应曲线，当K（刚度）,C（阻尼）,M（质量）变化时，频率响应曲线的变化情况。

图 1 单自由度系统刚度，阻尼，质量影响曲线

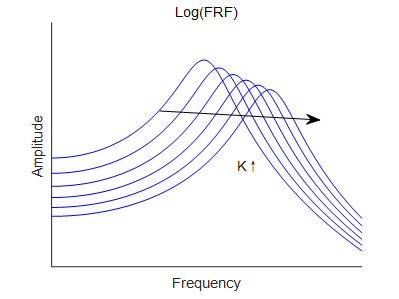
用图1放在文章中，不太美观，一看就是影印的，要是一般的文章还好，如果用来发表的就拉下档次了。所以就尝试了下重绘，重绘有两个方案，

（1）用PPT、visio或者Adobe Illustrator等绘图工具自己绘制

（2）用matlab先得到曲线的函数，进一步把函数显示出来

2. Visio绘制

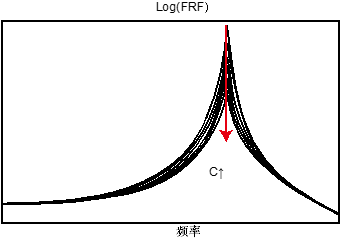
尝试了一下，质量变化影响曲线图相对还好画一些，但阻尼变化的曲线就不是那么容易画了，画出来总觉得差点意思。很难保证各曲线之间的间隔均匀；当然肯定是能做到，但自己非此方面的熟手，所以有两个解决方案，一个是尝试用Adobe Illustrator进行一定时间的专门学习，但时间成本太高；或者是淘宝上寻求供外包解决，也是能解决的；但最终我还是决定先尝试下第二种方案，先得到曲线的函数，然后用软件把函数绘出来。

  

图 2 Visio绘制曲线图

3. Matlab绘制

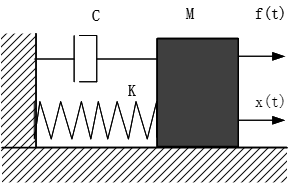
单自由度系统的物理模型如图 3 所示，

 

图 3单自由度系统模型

它的动力学方程为

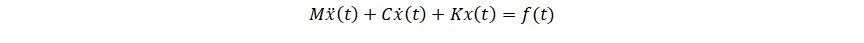
其中

$M$:质量; $C$:阻尼; $K$:刚度; $\ddot{x}$:加速度;$\dot{x}$:速度; $x$:位移; $f$:外力; $t$:时间。

这里的f(t)为脉冲激励：

使用汉宁窗生成：$ f(t<T_c)= \frac{A}{2} * cos(\frac{2*\pi* t(t<T_c)}{T_c}) $

% % 激励采用脉冲激励，脉冲激励为Hanning函数
function f = hanning_imp(t, Tc, A)
    f = zeros(size(t));
    f(t < Tc) = A / 2 * (1 - cos(2*pi * t(t < Tc) / Tc));
end

可以根据这个函数得到一个脉冲激励

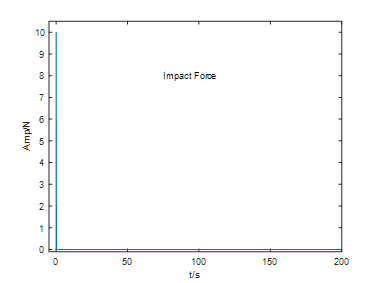
画图此图：

dt = 0.00001;
t = 0:dt:200;
Tc = 0.001;
A = 10;
u = hanning_imp(t, Tc, A);
plot(t,u,'LineWidth',1.5 );
axis([-5 200 -0.1 10.5 ]);
xlabel('t/s')
ylabel('Amp/N')
text(75,8,'Impact Force');

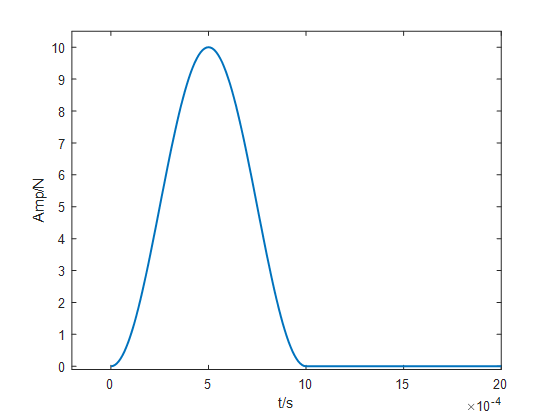
（a）整体图	(b)局部放大图
图 4 冲击力

建立系统方程，求解频率响应函数（FRF）

function [freq_x , amp_y]=frf_bing(m,k,c)

% m 质量
% k 刚度
% c 阻尼

num = 1;
den = [m c k];
sys = tf(num, den);

%采样频率(Hz) 100Hz 实际并不需要这么高的采样频率，但是如果采样时间太小，hanning脉冲不完整
% 为了得到准确的响应dt一定要小，否则做出的相位可能不对
dt = 0.00001;
fs = 1/dt;  

t = 0:dt:200;
Tc = 0.001;
A = 10;
u = hanning_imp(t, Tc, A);
y = lsim(sys, u, t);
y = y';

N = length(u);
fy = fft(y);
fu = fft(u);
ft = fy ./ fu;
f = (0:N-1) * fs ./ N;
ft_r = real(ft);
ft_i = imag(ft);

part = (f < 30);
freq_x=f(part);
amp_y= abs(ft(part));

End

(1) M变化时

取m=100,120,140,160,180,200分别绘制FRF的响应曲线。

clc;
clear;
close all;

%%
k = 1000;      %初始化k
c=100;         %初始化c
M=100:20:200;  %初始化m, 取m=100,120,140,160,180,200分别绘图

f1= figure(1);
hold on
    
for i= 1:length(M)
    [a(:,i) , b(:,i)]=frf_bing(M(i),k,c);
end

plot(a,log(b),'b');
axis([0 1 -8.2 -5.3]);
title('Log(FRF)');
xlabel('Frequency')
ylabel('Amplitude')
set(gca,'XTick',[],'YTick',[]);
text(0.3,-7,'M↑');
annotation('arrow',[0.7 0.3],[0.6 0.8]) ;
f1.Position=([ 0 0 400 300])

% 保存为emf 矢量格式
set(gcf,'unit','centimeters','position',[10 5 6.5 4.8]);
print(f1,'-dmeta','M.emf')

可以生成一幅想要的曲线，并且可以保存为矢量格式，无论放大多少倍，图片还是很清晰。

  

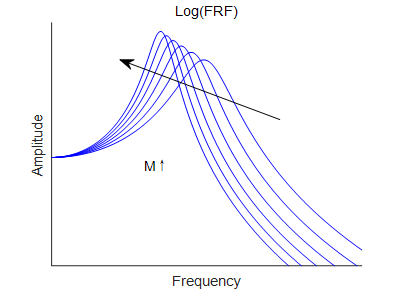图 5 质量变化的影响

(2)   K变化时

取K=1000,1200,1400,1600,1800,2000分别绘制FRF的响应曲线。

clc;
clear;
close all;

%%
k = 1000:200:2000;
c=100;
M=100;
f1= figure(1);
hold on
for i= 1:length(k)
[a(:,i) , b(:,i)]=frf_bing(M,k(i),c);
end

plot(a,log(b),'b');
axis([0 1 -8.2 -5.3]);
title('Log(FRF)');
xlabel('Frequency')
ylabel('Amplitude')
set(gca,'XTick',[],'YTick',[]);
text(0.6,-7,'K↑');
annotation('arrow',[0.4 0.8],[0.63 0.6]) ;
f1.Position=([ 0 0 400 300])

% 保存为emf 矢量格式
set(gcf,'unit','centimeters','position',[10 5 6.5 4.8]);
print(f1,'-dmeta','K.emf')

图 6刚度变化的影响

(3)   C变化时

取K=1000,1200,1400,1600,1800,2000分别绘制FRF的响应曲线。

clc;
clear;
close all;
%%

fontsizevalue=18;
c=100:20:200;
f1= figure(1);
hold on
for i= 1:length(c)
[a(:,i) , b(:,i)]=frf_bing(c(i));
end

plot(a,log(b),'b');
axis([0 1 -8 -5.5]);
t1=title('Log(FRF)');
xl=xlabel('Frequency')
y1=ylabel('Amplitude')
t1.FontSize =fontsizevalue;
y1.FontSize =fontsizevalue;
xl.FontSize =fontsizevalue;
set(gca,'XTick',[],'YTick',[]);
text(0.5,-7,'C↑');
annotation('arrow',[0.5 0.5],[0.9 0.5]) ;
f1.Position=([ 0 0 400 300])

% 保存为emf 矢量格式
set(gcf,'unit','centimeters','position',[10 5 6.5 4.8]);
print(f1,'-dmeta','K.emf')

 

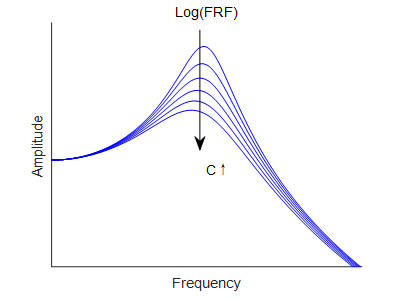图 7阻尼变化的影响

4.     参考文章

1. CSDN博主「whoispo」文 https://blog.csdn.net/WhoisPo/article/details/46865401