Python3解决棋盘覆盖问题的方法示例

本文实例讲述了Python3解决棋盘覆盖问题的方法。分享给大家供大家参考，具体如下：

问题描述：

在2^k*2^k个方格组成的棋盘中，有一个方格被占用，用下图的4种L型骨牌覆盖所有棋盘上的其余所有方格，不能重叠。

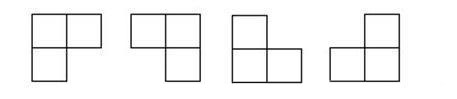
代码如下：

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

def chess(tr,tc,pr,pc,size):   global mark   global table   mark+=1   count=mark   if size==1:     return   half=size//2   if pr<tr+half and pc<tc+half:     chess(tr,tc,pr,pc,half)   else:     table[tr+half-1][tc+half-1]=count     chess(tr,tc,tr+half-1,tc+half-1,half)   if pr<tr+half and pc>=tc+half:     chess(tr,tc+half,pr,pc,half)   else:     table[tr+half-1][tc+half]=count     chess(tr,tc+half,tr+half-1,tc+half,half)   if pr>=tr+half and pc<tc+half:     chess(tr+half,tc,pr,pc,half)   else:     table[tr+half][tc+half-1]=count     chess(tr+half,tc,tr+half,tc+half-1,half)   if pr>=tr+half and pc>=tc+half:     chess(tr+half,tc+half,pr,pc,half)   else:     table[tr+half][tc+half]=count     chess(tr+half,tc+half,tr+half,tc+half,half) def show(table):   n=len(table)   for i in range(n):     for j in range(n):       print(table[i][j],end=' ')     print('') mark=0 n=8 table=[[-1 for x in range(n)] for y in range(n)] chess(0,0,2,2,n) show(table)

n是棋盘宽度，必须是2^k，本例中n=8，特殊格子在(2,2)位置，如下图所示：

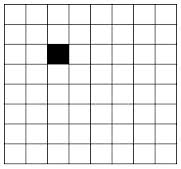
采用分治法每次把棋盘分成4份，如果特殊格子在这个小棋盘中则继续分成4份，如果不在这个小棋盘中就把该小棋盘中靠近中央的那个格子置位，表示L型骨牌的1/3占据此处，每一次递归都会遍历查询4个小棋盘，三个不含有特殊格子的棋盘置位的3个格子正好在大棋盘中央构成一个完整的L型骨牌，依次类推，找到全部覆盖方法。运行结果如下：

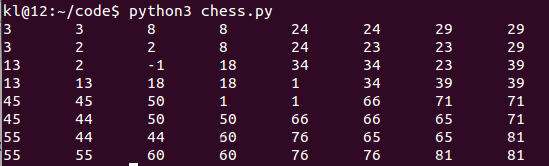
希望本文所述对大家Python程序设计有所帮助。