最短路径问题,BFS,408方向,思路与实现分析

继上回挖下的坑,不知道大家有没有认真看最小生成树呢?很简单,这回也讲讲正常难度的,看不懂就来这里看看,讲的很好~~

最短路径问题

说起这个问题,先说个问题吧~~

这回不修路了,这回运东西哈哈哈,abcde五个城市,a是丝绸产业重地,那么经常要往,bcde4个城市运东西,那么到各个城市怎么运送距离最近呢?图示见下~~

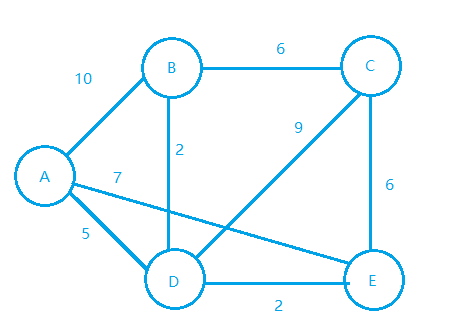
a分别到各个城市运送,这是一个单源最短路径问题~~

那么如果各个城市之间都有特产,需要相互的两两之间运送距离最近呢?这就是各顶点之间的最短路径问题~

所以明确一下,要搞的这三个算法当然是有适用范围的~~

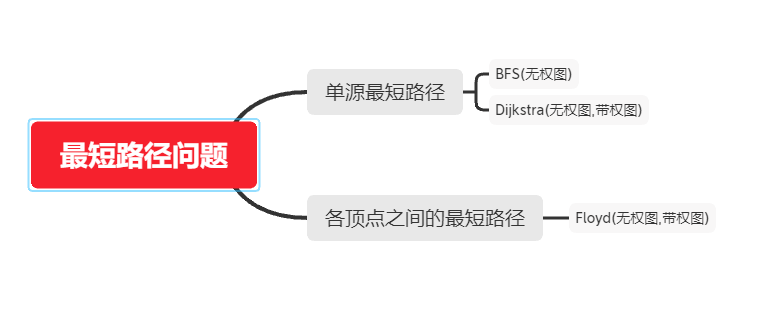
单源最短路径-BFS求无权图思路

BFS其实也就是广度优先遍历,图的广度优先遍历这里我们来模拟一下~~

当然,无权图你也可以想象成权值为一的特殊带权图嘛~~

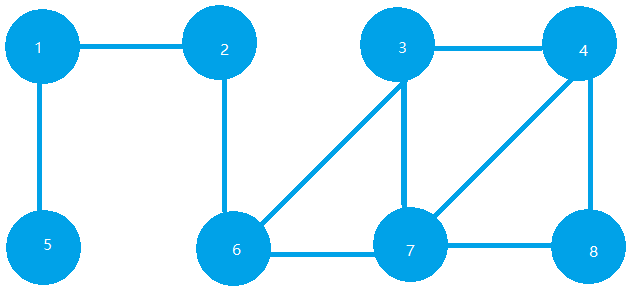
第一次遍历,我们访问的元素应该是1和6~~

第二次遍历,我们访问的元素应该是5,3和7~~

第三次遍历,我们访问的元素应该是4和8~~

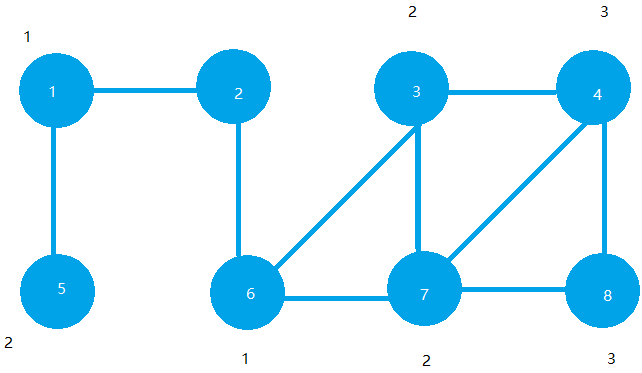
BFS代码实现与分析

先来代码~~

void BFS_MIN_Distance(Graph G,int u)

{

    for(i = 0;i < G.vexnum; ++i)

    {

     	d[i] =  false; //单源到各点路径长度的最短路径,先初始化,false代表不可到达

        path[i] = -1;  //最短路径从哪个顶点过来,先初始化

    }

    d[u] = 0;

    visited[u] =TRUE; //标记顶点u已被标记

    EnQueue(Q,u);//顶点u入队列

    while(!isEmpty(Q))//主过程

    {

        DeQueue(Q,u);//顶点u出队列

        for(w = FirstNeighbor(G,u); w >= 0; w = NextNeighbor(G,u,w))

        {	//遍历当前出队列的元素的所有邻接顶点,第一次为遍历顶点u的所有邻接顶点

            //当前出队列的元素即跳出for循环之后,再进入for循环时,本例中,u即为1号元素

            if(!visited[w]) //w为u为尚未访问的邻接顶点

            {

                d[w] = d[u] +1;//路径长度加1

                path[w] = u; //最短路径为u到w

                visited[w] = TRUE;//标记顶点w已被标记

                EnQueue(Q,w);//顶点w入队列

            }

        }

    }

}

我们需要列出3块内容帮助我们分析~~

visited数组:

	1	2	3	4	5	6	7	8
visited	false	false	false	false	false	false	false	false

队:开始的时候没有元素~~

d[]和path[]数组

	1	2	3	4	5	6	7	8
d[]	false	false	false	false	false	false	false	false
path[]	-1	-1	-1	-1	-1	-1	-1	-1

分析一下到while主过程之前,我们做的事情~~

visited数组:

	1	2	3	4	5	6	7	8
visited	false	true	false	false	false	false	false	false

队: 2 ,u为2

d[]和path[]数组

	1	2	3	4	5	6	7	8
d[]	false	0	false	false	false	false	false	false
path[]	-1	-1	-1	-1	-1	-1	-1	-1

那么此时进入while循环~~

第一次while循环,2出队~~

队: 空,此时2出队了~~

进入for循环~~

第一次for,u为2,第一个邻接顶点为1,并且1尚未访问,所以路径长度加1,最短路径为u到w,即2到1,标记1已访问,1入队,w=NextNeighbor,还有邻接顶点,所以继续~~

第二次for,第二个u的邻接顶点,为6,并且6尚未访问所以路径长度加1,最短路径为u到w,即2到6,标记6已访问,6入队,w=NextNeighbor,没有邻接顶点了所以跳出~~

此时

visited数组:

	1	2	3	4	5	6	7	8
visited	true	true	false	false	false	true	false	false

队: 1,6 ,队头为1,所以u为1

d[]和path[]数组

	1	2	3	4	5	6	7	8
d[]	1	0	false	false	false	1	false	false
path[]	2	-1	-1	-1	-1	2	-1	-1

第二次while

1出队~~

进入for循环~~

第一次for,u为1,第一个邻接顶点为2,但是2已被访问,所以不执行if内语句,w=NextNeighbor,还有邻接顶点,所以继续~~

第二次for,第二个u的邻接顶点,为5,5尚未访问所以路径长度加1,此时因为d[u]初始为1,所以为1+1=2,最短路径为u到w,即1到5,标记5已访问,5入队,w=NextNeighbor,没有邻接顶点了所以跳出~~

此时

visited数组:

	1	2	3	4	5	6	7	8
visited	true	true	false	false	true	true	false	false

队: 6 ,5,队头为6,所以u为6

d[]和path[]数组

	1	2	3	4	5	6	7	8
d[]	1	0	false	false	2	1	false	false
path[]	2	-1	-1	-1	1	2	-1	-1

第三次while~~

6出队,再进行for循环,那么之后就会变成~~

visited数组:

	1	2	3	4	5	6	7	8
visited	true	true	true	false	true	true	true	false

队: 5,3,7队头为5,所以u为5

d[]和path[]数组

	1	2	3	4	5	6	7	8
d[]	1	0	2	false	2	1	2	false
path[]	2	-1	6	-1	1	2	6	-1

第四次whlie~~

5,出队,再进行for,没有邻接顶点,所以没有改变~~

visited数组:

	1	2	3	4	5	6	7	8
visited	true	true	true	false	true	true	true	false

队: 3,7队头为3,所以u为3

d[]和path[]数组

	1	2	3	4	5	6	7	8
d[]	1	0	2	false	2	1	2	false
path[]	2	-1	6	-1	1	2	6	-1

第五次while~~

3出队,进行for,此时~~

visited数组:

	1	2	3	4	5	6	7	8
visited	true	true	true	true	true	true	true	false

队: 7队头为7,所以u为7

d[]和path[]数组

	1	2	3	4	5	6	7	8
d[]	1	0	2	3	2	1	2	false
path[]	2	-1	6	3	1	2	6	-1

第六次whlie~~

7出队,进行for,此时~~

visited数组:

	1	2	3	4	5	6	7	8
visited	true	true	true	true	true	true	true	true

队: 没有元素入队,队空了~~

d[]和path[]数组

	1	2	3	4	5	6	7	8
d[]	1	0	2	3	2	1	2	3
path[]	2	-1	6	3	1	2	6	7

此时队空,跳出while,执行成功~~

此时,我们得到了d[]和path[]数组~~

	1	2	3	4	5	6	7	8
d[]	1	0	2	3	2	1	2	3
path[]	2	-1	6	3	1	2	6	7

比如我们看4号元素,即可知~~

2到4号元素的最短路径为长度d[4] = 3;

2到4号元素的最短路径为: 看4号元素path[4]为3,4 <- 3,再看3号元素path[3]为6,3 <- 6 ,再看6号元素path[6]为2,6 <- 2,所以2到4的最短路径为:2 -> 6 -> 3 -> 4~~

写到这才发现一写就挺多的,那Dijkstra,Floyd算法就下次再写咯~~