「题解」HDU-4015 Mario and Mushrooms

本文将同步发布于：

• 洛谷博客；
• csdn；
• 博客园；
• 简书；

题目

题目链接：HDU-4015 Mario and Mushrooms、Vjudge HDU-4015。

题意简述

马里奥初始只有 \(1\) 点血。

有两种蘑菇，一种是好蘑菇，一种是坏蘑菇；好的吃了会增加 \(1\) 点血，坏蘑菇吃了会减少 \(m\) 点血；

共有 \(mk+1\) 个好蘑菇和 \(k\) 个坏蘑菇，请问有多少种蘑菇的排列方式使得马里奥在按顺序吃下蘑菇后的任意时刻血量均 \(\geq 1\)。

求答案与总的排列个数的比值，即马里奥的存活概率。

两个排列不同，当且仅当存在至少一个位置蘑菇的种类不同。

题解

Raney 引理

不难发现，如果马里奥可以存活，那么最后吃完所有蘑菇，一定只剩下 \(1\) 点血。

不难考虑到 Raney 引理，即对于一个总和为 \(1\) 的整数序列，它的循环同构序列中有且仅有一个满足前缀和数组均大于 \(0\)。

证明：

具体地，我们考虑在平面直角坐标系 \(xOy\) 中绘制前缀和数列图像（以 \(a=[1,3,-4,1]\) 为例）。

作一条斜率为 \(\frac{1}{a+b}\) 的直线，将其平移到与图像下相切。

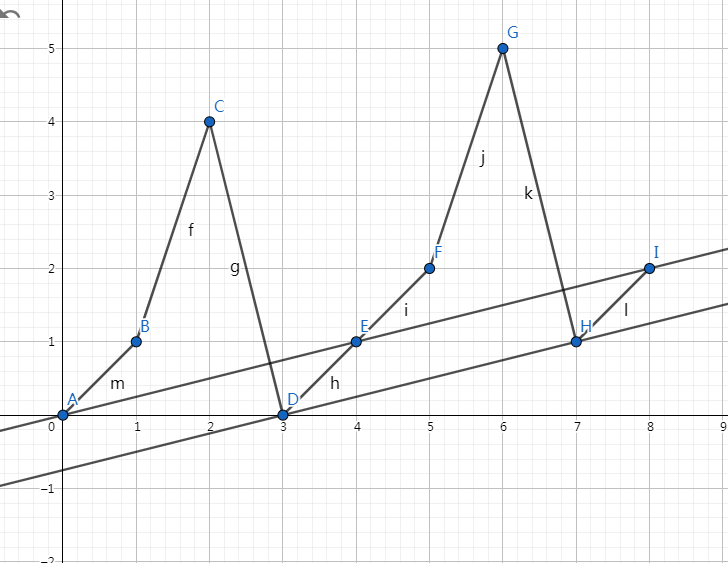
• 充分性：不难发现，如果我们以切点为循环位移的终点（它后一个点为数列的第一项），构造出来的数列一定符合条件；
• 必要性：如果不相切，必定存在交点，考虑到数列中都是整数，交点一定满足纵坐标小于等于切点，前缀和小于等于零，不可能。

Raney 引理得证。

圆排列与计数

由 Raney 得知，所有蘑菇的一个圆排列一定对应恰好一个合法的排列，因此我们要求解的实际上就是圆排列个数与总排列个数的比值。

根据重复元素排列公式：

总的排列个数 \(p\) 满足

\[p=\frac{(k+mk+1)!}{k!(mk+1)!}
\]

根据圆排列公式：

圆排列个数 \(q\) 满足

\[q=\frac{p}{k+mk+1}
\]

因此，答案 \(\texttt{ans}\) 满足

\[\texttt{ans}=\frac{q}{p}=\frac{1}{k+mk+1}
\]

参考代码

#include<cstdio>
using namespace std;
#define reg register
typedef long long ll;

int main(void){
	int t;
	scanf("%d",&t);
	reg int Case=0;
	while(t--){
		static int m,k;
		scanf("%d%d",&m,&k);
		printf("Case #%d: %.8lf\n",++Case,1.0/(k+m*k+1));
	}
	return 0;
}