LuoguP4420 [COCI2017-2018#1] Tetris 题解

Content

有一个 \(n\times m\) 的拼图，摆上了几块俄罗斯方块图形。已知这些图形可能包含以下这五种（可以旋转），求出下列类型的俄罗斯方块图形数量。

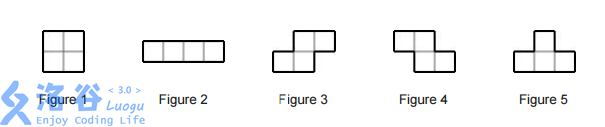
数据范围：\(1\leqslant n,m\leqslant 10\)。

Solution

像我这样菜的人，这种题目只有一种方法：暴力判断。

各位玩过俄罗斯方块的都知道，上面 \(5\) 种图形中，第一种图形无论怎么旋转都是一样的，第二、三、四种都可以通过旋转得到两种不同的图形，第五种可以通过旋转得到 \(4\) 种不同的图形。具体是什么样的想必各位都能够想象得出来。

于是，我们只需要对这总共 \(1+2\times 3+4=11\) 种情况进行暴力判断就好了。抓住这些图形的特征，并转化成代码语言就能够迎刃而解。

然而最烦人的就是打代码的过程……

Code

仅搬出判断五种不同类型的图形的函数 \(\texttt{judge1}\sim\texttt{judge5}\)，毕竟这才是整个代码的精髓，也是我打得最要命的地方……

inline bool judge1(int i, int j) {return a[i][j] != '.' && (a[i][j] == a[i + 1][j] && a[i][j] == a[i + 1][j + 1] && a[i][j] == a[i][j + 1]);}
inline bool judge2(int i, int j) {return a[i][j] != '.' && ((a[i][j] == a[i][j + 1] && a[i][j] == a[i][j + 2] && a[i][j] == a[i][j + 3]) || (a[i][j] == a[i + 1][j] && a[i][j] == a[i + 2][j] && a[i][j] == a[i + 3][j]));}
inline bool judge3(int i, int j) {return a[i][j] != '.' && ((a[i][j] == a[i][j - 1] && a[i][j] == a[i + 1][j - 1] && a[i][j] == a[i + 1][j - 2]) || (a[i][j] == a[i + 1][j] && a[i][j] == a[i + 1][j + 1] && a[i][j] == a[i + 2][j + 1]));}
inline bool judge4(int i, int j) {return a[i][j] != '.' && ((a[i][j] == a[i][j + 1] && a[i][j] == a[i + 1][j + 1] && a[i][j] == a[i + 1][j + 2]) || (a[i][j] == a[i + 1][j] && a[i][j] == a[i + 1][j - 1] && a[i][j] == a[i + 2][j - 1]));}
inline bool judge5(int i, int j) {return a[i][j] != '.' && ((a[i][j] == a[i + 1][j - 1] && a[i][j] == a[i + 1][j] && a[i][j] == a[i + 1][j + 1]) || (a[i][j] == a[i - 1][j - 1] && a[i][j] == a[i][j - 1] && a[i][j] == a[i + 1][j - 1]) || (a[i][j] == a[i - 1][j - 1] && a[i][j] == a[i - 1][j] && a[i][j] == a[i - 1][j + 1]) || (a[i][j] == a[i - 1][j + 1] && a[i][j] == a[i][j + 1] && a[i][j] == a[i + 1][j + 1]));}