题解-Atcoder_agc005D ~K Perm Counting

Problem

AtCoder-agc005D

题意概要：给出\(n,k\)，求合法的排列个数，其中合法定义为任何数字所在位置与自身值差的绝对值不为\(k\)（即求排列\(\{A_i\}\)，使得\(\forall i\in[1,n],|a_i-i|\not =k\)

Solution

刚看这道题时除了全集取反搞容斥外没有任何思路啊

\(f_i\)表示排列中至少有\(i\)对冲突的方案数，一对冲突定义为存在一个\(i\)使得\(|a_i-i|=k\)

考虑全集取反，加上一点点容斥思想可得

\[Ans=\sum_{i=0}^n(-1)^i\cdot P_n^i\cdot f_i
\]

至于怎么得到 \(f_i\)，就是这道题难点所在，关键思路是画图

构建一个二分图：

• 其中 \(i\) 为数值 \(i\)，\(i'\) 为 \(i\) 在排列中的位置编号
• 构建边为冲突，即所有 \(i'\) 要和 \(i\pm k\) 连边

就像这样（模拟 \(n=4,k=1\) 的情况）：

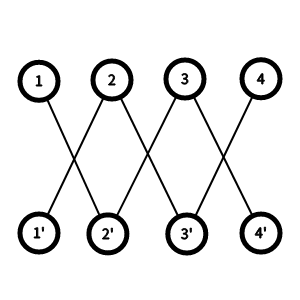
发现这个二分图中其实只有\(2k\)条链，于是可以对这\(2k\)条链进行Dp

在某条链上：设\(g[i][j][0/1]\)表示考虑前\(i\)个点，且已经有\(j\)对冲突，\(i\)号与\(i+1\)号连与不连的方案数，得出转移方程：

\[g[i][j][0]=g[i-1][j][0]+g[i-1][j][1]\\g[i][j][1]=g[i-1][j-1][0]
\]

对于每条链的\(f[i]\)即为\(g[end][i][0]+g[end][i][1]\)（\(end\)为链的末尾），最后合并\(2k\)条链的时候可以玩背包

但实际上有个小技巧，就是将\(2k\)条链首尾顺次相接，在两条链的交界处不转移第二个方程即可

Code

#include <cstdio>

const int N=2040,p=924844033;
int f[N+N][N][2];
bool end[N+N];
int n,k,Ans,fac[N];

inline int qm(int x){return x<p?x:x-p;}

int main(){
	scanf("%d%d",&n,&k);fac[0]=1;
	for(int i=1;i<=n;++i)fac[i]=1ll*fac[i-1]*i%p;
	for(int i=1,tt=0,d;i<=k;++i){
		d=(n-i)/k+1;
		tt+=d,end[tt]=true;
		tt+=d,end[tt]=true;
	}
	f[1][0][0]=1;
	for(int i=1;i<=n+n;++i)
	for(int j=0;j<=n;++j){
		f[i+1][j][0]=qm(f[i][j][0]+f[i][j][1]);
		if(!end[i])f[i+1][j+1][1]=f[i][j][0];
	}
	for(int i=0,t;i<=n;++i){
		t=1ll*fac[n-i]*qm(f[n+n][i][0]+f[n+n][i][1])%p;
		if(i&1)Ans=qm(Ans-t+p);
		else Ans=qm(Ans+t);
	}
	printf("%d\n",Ans);
	return 0;
}