强联通分量-tarjan算法

定义：在一张有向图中，两个点可以相互到达，则称这两个点强连通；一张有向图上任意两个点可以相互到达，则称这张图为强连通图；非强连通图有极大的强连通子图，成为强联通分量。

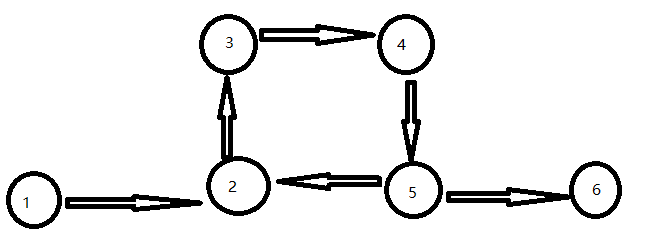
如图，{1}，{6}分别是一个强连通分量，{2,3,4,5}是一个强连通分量。而Tarjan算法可用于求解强连通分量。

---

Tarjan算法：

Tarjan算法是基于深度优先搜索的算法，每个强连通分量都是搜索树中的一个子树。

实现：dfn[u]表示到u节点时的标记（时间戳），low[u]表示u所能走到的节点中，点的最小的次序号（dfn），每搜寻一个节点u，就把一个节点入栈，令dfn[u]=++it;low[u]=dfn[u]。u所连接的节点为v，若v已经被搜寻过，则low[u]=min(low[u],low[v])。若v没有被搜寻过，则dfs（v）low[u]=min(low[u],low[v])。搜寻完u所连接的所有的边后，若dfn[u]==low[u]，则u这个点是该点所在强连通分量中编号最小的点。此时栈里的u节点上面的全部为该强连通分量的节点。

第一步：

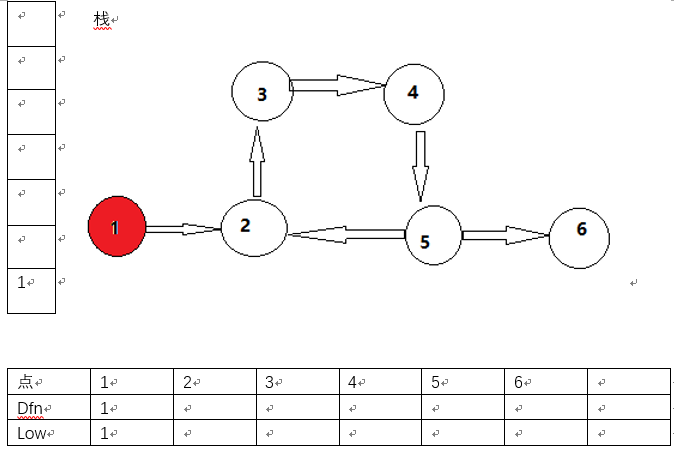
点1有一条边指向2号点，而且2号点没有被遍历，dfs(2)。

第二步

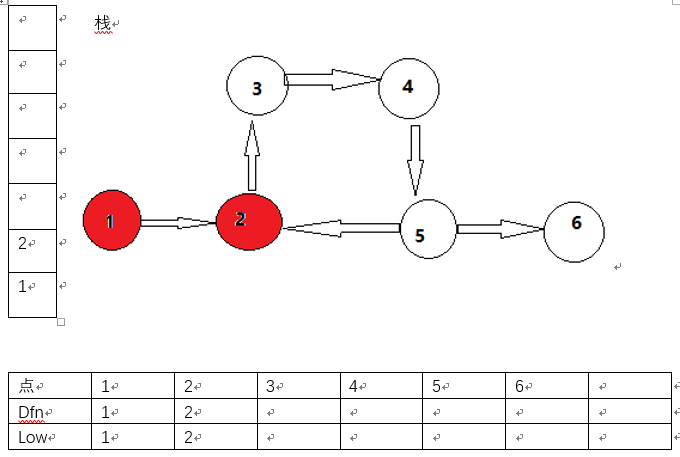
2有一条边指向3，遍历三号点。

第三步：

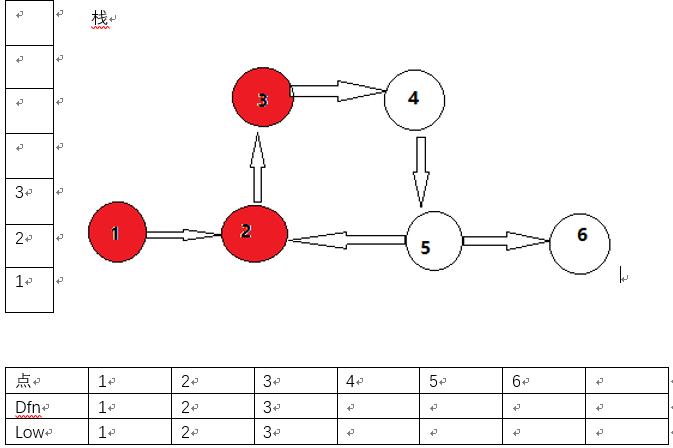
3指向4，dfs(4)。

第四步：

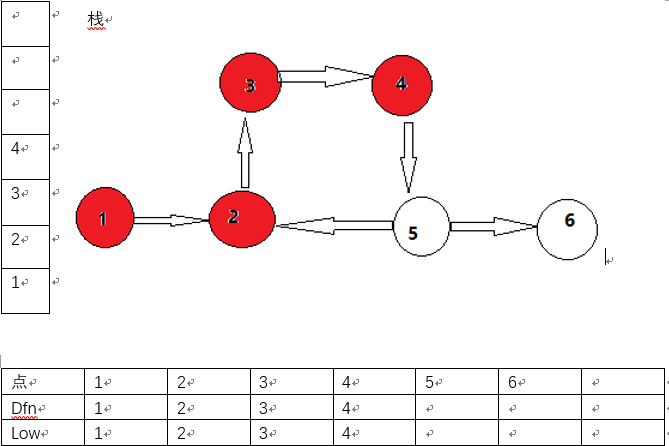
dfs(5)。

第五步：

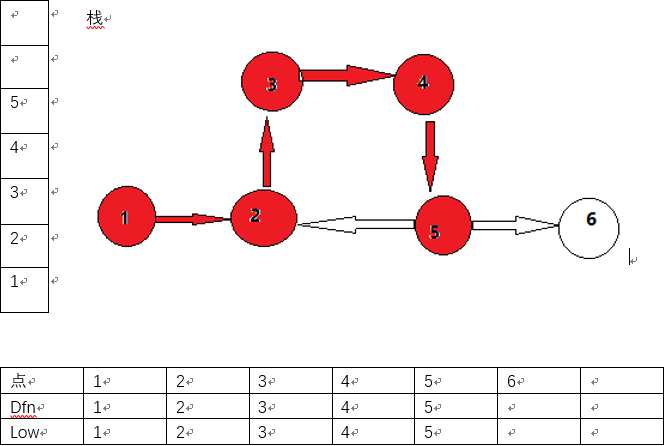
5号点存在两条边，两条边都要遍历，假设先走到2号点的边。因为2号点已经遍历过，所以直接比较即可，这时候要更新5号点的low。

第六步：

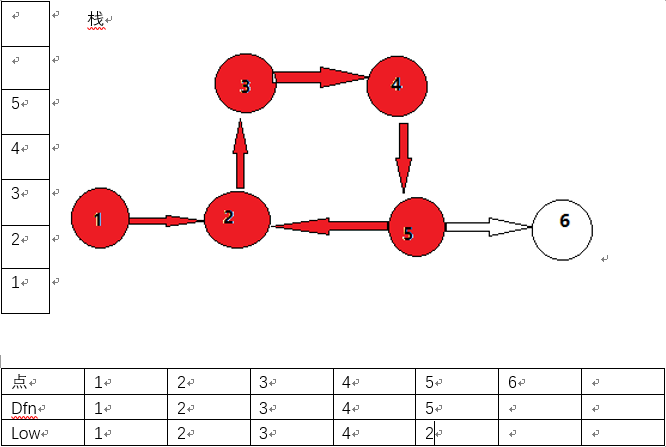
然后遍历6号节点。

第七步：

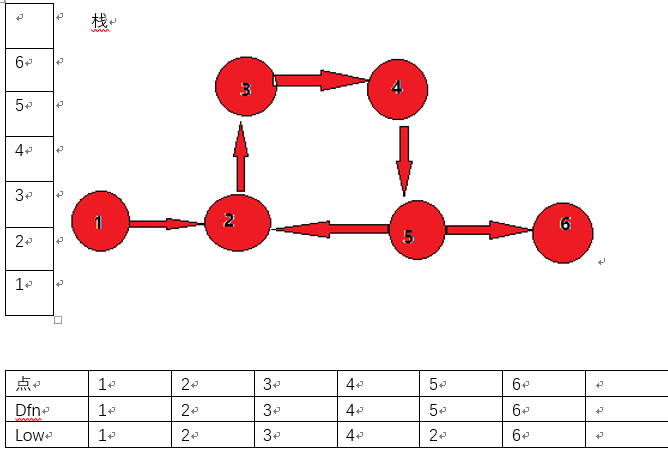
此时6号节点无法向外扩展节点，此时dfn[6]==low[6]，因此6号节点就是一个强连通分量。弹出6号节点，回溯。此时图的遍历已经完成，所有的节点均已被打上标记。

第八步：

回溯到5号节点，low[5]!=dfn[5]，继续回溯。

第九步：

回溯到4号节点，更新4号节点的low值。

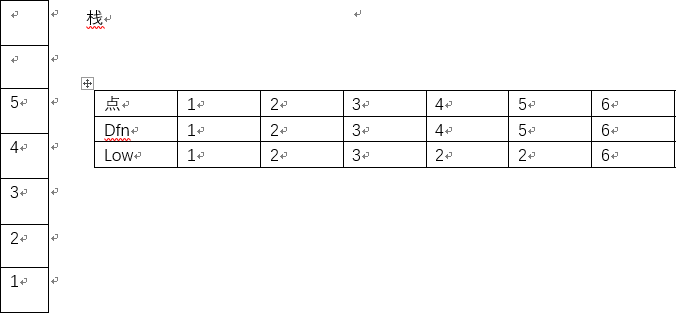
第十步：

回溯到3号节点，更新3号的low值。

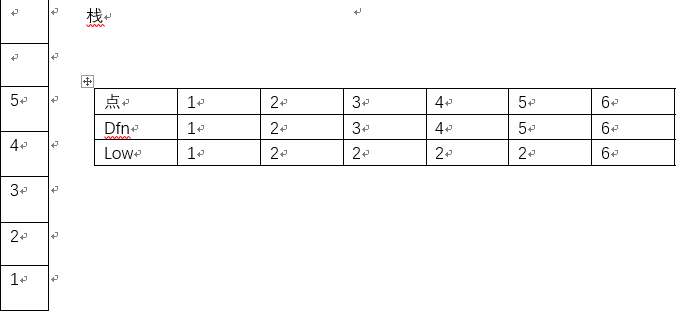
第十一步：

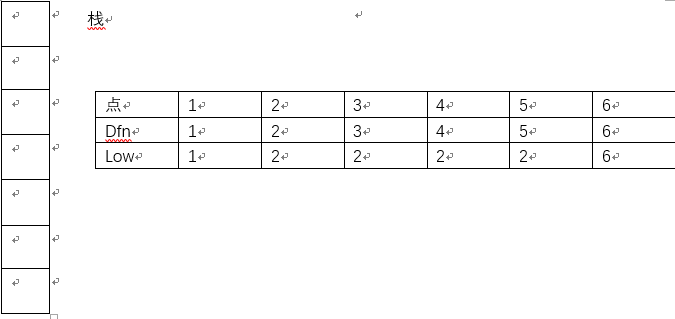
回溯到2号节点，此时low[2]==dfn[2]，因此，栈中2号点上面的（包括2号点）全部在一个强连通分量中。将他们全部弹出。

第十二步：

回溯到1号节点，dfn[1]==low[1]，因此1号节点也是一个强连通分量。弹出。

void tarjan(int u){
    dfn[u]=++it;
    low[u]=it;
    for(int i=;i<tu[u].size();i++){
        if(!in[tu[u][i]]){
            in[tu[u][i]]=true;
            s.push(tu[u][i]);
            tarjan(tu[u][i]);
            low[u]=min(low[u],low[tu[u][i]]);
        }
        else{
            low[u]=min(low[u],low[tu[u][i]]);
        }
    }
    if(low[u]==dfn[u]){
        while(s.top()!=u){
            s.pop();
        }
        s.pop();
    }
}