『科学计算_理论』优化算法：梯度下降法&牛顿法

梯度下降法

梯度下降法用来求解目标函数的极值。这个极值是给定模型给定数据之后在参数空间中搜索找到的。迭代过程为：

可以看出，梯度下降法更新参数的方式为目标函数在当前参数取值下的梯度值，前面再加上一个步长控制参数alpha。梯度下降法通常用一个三维图来展示，迭代过程就好像在不断地下坡，最终到达坡底。为了更形象地理解，也为了和牛顿法比较，这里我用一个二维图来表示：

懒得画图了直接用这个展示一下。在二维图中，梯度就相当于凸函数切线的斜率，横坐标就是每次迭代的参数，纵坐标是目标函数的取值。每次迭代的过程是这样：

1. 首先计算目标函数在当前参数值的斜率（梯度），然后乘以步长因子后带入更新公式，如图点所在位置（极值点右边），此时斜率为正，那么更新参数后参数减小，更接近极小值对应的参数。
2. 如果更新参数后，当前参数值仍然在极值点右边，那么继续上面更新，效果一样。
3. 如果更新参数后，当前参数值到了极值点的左边，然后计算斜率会发现是负的，这样经过再一次更新后就会又向着极值点的方向更新。

根据这个过程我们发现，每一步走的距离在极值点附近非常重要，如果走的步子过大，容易在极值点附近震荡而无法收敛。解决办法：将alpha设定为随着迭代次数而不断减小的变量，但是也不能完全减为零。

梯度下降法实战

我们来求解Ax=b，程序如下：

%matplotlib inline
import copy
import numpy as np
import matplotlib.pyplot as plt

A = np.array([[4,2],[1,3]])
b = np.array([[3],[2]])

loss = []
x0 = [copy.deepcopy([]), copy.deepcopy([])]
step = 0.01
x = [[0.],[4]]

while (A.dot(x)-b).T.dot(A.dot(x)-b) > 0.1:
    dx = 2*A.T.dot(A).dot(x) - 2*A.T.dot(b)
    x = x - step*dx
    x0[0].append(x[0])
    x0[1].append(x[1])
    loss.append(np.squeeze((A.dot(x)-b).T.dot(A.dot(x)-b)))

line = np.linspace(0,len(x0[0])-1,len(x0[0]))

fig,(ax0,ax1)=plt.subplots(2,1, figsize=(9,6))
ax1.plot(line, x0[0])
ax1.plot(line, x0[1])
ax0.plot(line, loss)
ax1.plot(line, np.ones(len(x0[0]))*0.5)
plt.show

上图表示loss函数的降低趋势，下图反映了解的收敛趋势：

牛顿法

首先得明确，牛顿法是为了求解函数值为零的时候变量的取值问题的，具体地，

一阶方法：

当要求解 f(θ)=0时，如果 f可导，那么可以通过迭代公式

来迭代求得最小值。通过一组图来说明这个过程。

二阶方法：

当应用于求解最大似然估计的值时，变成ℓ′(θ)=0的问题。这个与梯度下降不同，梯度下降的目的是直接求解目标函数极小值，而牛顿法则变相地通过求解目标函数一阶导为零的参数值，进而求得目标函数最小值。那么迭代公式写作：

当θ是向量时，牛顿法可以使用下面式子表示：

其中H叫做海森矩阵，其实就是目标函数对参数θ的二阶导数。

通过比较牛顿法和梯度下降法的迭代公式，可以发现两者及其相似。海森矩阵的逆就好比梯度下降法的学习率参数alpha。牛顿法收敛速度相比梯度下降法很快，而且由于海森矩阵的的逆在迭代中不断减小，起到逐渐缩小步长的效果。

牛顿法的缺点就是计算海森矩阵的逆比较困难，消耗时间和计算资源。因此有了拟牛顿法。

实践练习

%matplotlib inline
import copy
import numpy as np
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

A = np.array([[4,2],[1,3]])
b = np.array([[3],[2]])

X, Y = np.meshgrid(np.linspace(-10, 10, 200),np.linspace(-10, 10, 200))

def get_loss(X,Y):
    Z = (A[0,0]**2+A[1,0]**2)*X**2 + (A[0,1]**2+A[1,1]**2)*Y**2 - 2*(A[0,0]*A[0,1]+A[1,0]*A[1,1])*X*Y - 2*(A[0,0]*b[0]+A[1,0]*b[1])*X \
            - 2*(A[0,1]*b[0]+A[1,1]*b[1])*Y
    return Z

Z = get_loss(X,Y)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X,Y,Z,rstride=5, cstride=5, alpha=0.3)
ax.contour(X,Y,Z, alpha=0.3)
cset = ax.contour3D(X, Y, Z, 10, zdir='z', offset=-100, cmap=cm.coolwarm)

# 梯度下降法
step = 0.01
x_g = np.array([[0],[-4]])
for i in range(100):
    dx_g = 2*A.T.dot(A).dot(x_g[:,-1].reshape(2,1)) - 2*A.T.dot(b)
    x_g = np.concatenate((x_g,x_g[:,-1].reshape(2,1) - step*dx_g),axis=1)
z_g = get_loss(x_g[0],x_g[1])
ax.plot(x_g[0],x_g[1],z_g,'ro')

# 牛顿法
# 黑塞矩阵
H = np.matrix([[A[0,0]**2+A[1,0]**2,         A[0,0]*A[0,1]+A[1,0]*A[1,1]],
               [A[0,0]*A[0,1]+A[1,0]*A[1,1],        A[0,1]**2+A[1,1]**2]],dtype='float64') * 2
x_n = np.array([[0.],[-4.]])
for i in range(100):
    dx_n = 2*A.T.dot(A).dot(x_n[:,-1].reshape(2,1)) - 2*A.T.dot(b)
    x_n = np.concatenate((x_n, x_n[:,-1] - np.linalg.inv(H).dot(dx_n)),axis=1)
z_n = get_loss(np.squeeze(np.asarray(x_n[0])),np.squeeze(np.asarray(x_n[1])))
ax.plot(np.squeeze(np.asarray(x_n[0])),np.squeeze(np.asarray(x_n[1])),z_n,'go')

f, (ax1, ax2) = plt.subplots(1, 2)
ax1.plot(np.linspace(0,len(z_g)-1,len(z_g)),z_g,'b',label='grad')
ax1.plot(np.linspace(0,len(z_n)-1,len(z_n)),z_n,'r',label='Newton')
ax1.legend()

cs = ax2.contour(X,Y,Z)
ax2.clabel(cs, inline=1, fontsize=5)
ax2.plot(np.squeeze(np.asarray(x_n[0])),np.squeeze(np.asarray(x_n[1])),'b')
ax2.plot(x_g[0],x_g[1],'r')

程序学习：

尝试了平面等高线图和线标注的绘制，

cs = ax2.contour(X,Y,Z)

ax2.clabel(cs, inline=1, fontsize=5)

注意到数组拼接方法都是不破坏原数组，单纯返回新数组的，且axis=0是行拼接（行数增加），axis=1是列拼接（列数增加），

x_n = np.concatenate((x_n, x_n[:,-1] - np.linalg.inv(H).dot(dx_n)),axis=1)

学习了numpy中的矩阵类型：np.matrix()，在牛顿法中我用的是matrix，在梯度下降法中我用的是array：

matrix是array的子类，特点是有且必须只是2维，matrix.I()可以求逆，和线代的求逆方法一致，所以绘图时我不得不才用np.sequeeze(np.asarray())操作来降维，而由于x[:, -1]这种操作对array会自动降维（由两行变为一行），所以要么使用matrix，要么切片后reshape(2,1)，总之不消停。

结果分析：

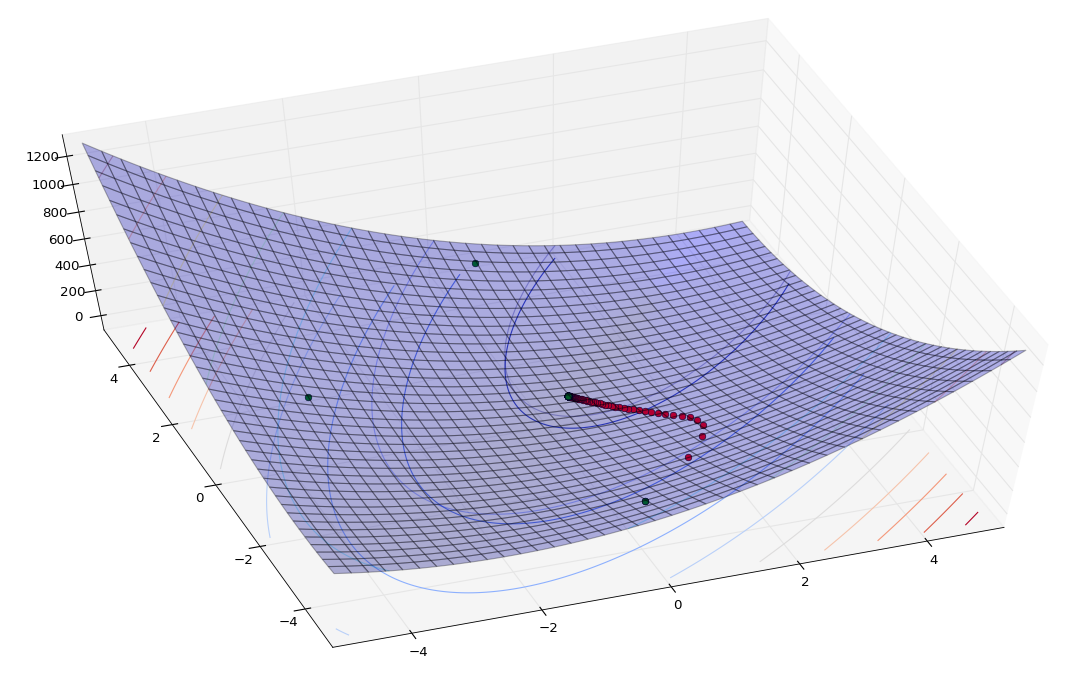
从两张角度截一下图，红色是梯度下降蓝色是牛顿法，可以看到，牛顿法收敛速度很快（外围只有3个点），不过这是建立在黑塞矩阵的基础上（需要求解目标函数的二阶偏导数），这是牛顿法快速收敛的原因，也是牛顿法的瓶颈，而且这个瓶颈很直观：我计算黑塞矩阵的numpy矩阵表达方法时的确费了挺大劲（其实原因更多是我渣... ...）