【Luogu】P2762太空飞行计划（最大权闭合图）

　　题目链接

　　woc这题目的输入格式和输出格式真的恶心

　　首先我们就着样例讲一下闭合图

　　

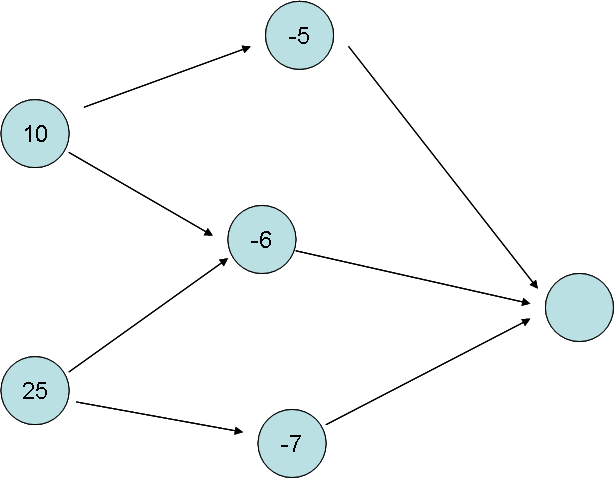
　　如图所示，第一层是两个实验节点，带来正收益；第二层是三个仪器节点，带来负收益；问讲道理到终点可以获得多大收益。

　　闭合图是什么呢？闭合图是一个点集，这个点集中所有点的出边所指向的点都必须在闭合图中。我们用点权来表示点的话，比如点集{10，-5，-6，终点}就是个闭合图，然而{10,25}就不是。

　　然后这题显而易见的叫我们求出最大权闭合图。

　　于是我们可以把它变成这样一个图：

　　

　　如图，从源点到每个正点权点连一条容量为点权的边，从正点权点向负点权点连一条容量为INF的边，再从负点权点向汇点连一条容量是该点点权绝对值的边。

　　这样原来的求最大权闭合图变成求这个图的最小割。证明在这边

　　这样就完啦

　　

#include<cstdio>
#include<cstring>
#include<cctype>
#include<cstdlib>
#include<algorithm>
#include<iostream>
#include<queue>
#define maxn 1000
#define maxm 1000
using namespace std;

inline long long read(){
    long long num=,f=;
    char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-')    f=-;
        ch=getchar();
    }
    while(isdigit(ch)){
        num=num*+ch-'';
        ch=getchar();
    }
    return num*f;
}

inline int count(int i){    return i&?i+:i-;    }

struct Edge{
    int next,to,val;
}edge[maxm*];
int head[maxn*],num;
inline void addedge(int from,int to,int val){
    edge[++num]=(Edge){head[from],to,val};
    head[from]=num;
}
inline void add(int from,int to,int val){
    addedge(from,to,val);
    addedge(to,from,);
}

bool vis[maxn*];
int dfn[maxn];
int dis[maxn];
bool ext[maxn];
int list[maxn];
int Start,End;
bool bfs(){
    memset(vis,,sizeof(vis));
    memset(dis,,sizeof(dis));
    queue<int>f;
    f.push(Start);vis[Start]=;dfn[Start]=;
    while(!f.empty()){
        int from=f.front();f.pop();
        for(int i=head[from];i;i=edge[i].next){
            int to=edge[i].to;
            if(edge[i].val<=||vis[to])    continue;
            dfn[to]=dfn[from]+;    vis[to]=;    dis[to]=dis[from]+;
            f.push(to);
        }
    }
    return vis[End];
}

int dfs(int x,int val){
    //printf("%d\n",x);
    if(x==End||val==)    return val;
    int flow=;vis[x]=;
    for(int &i=list[x];i;i=edge[i].next){
        int to=edge[i].to;
        if(edge[i].val<=||dfn[to]!=dfn[x]+||vis[to])    continue;
        int now=dfs(to,min(val,edge[i].val));
        edge[i].val-=now;edge[count(i)].val+=now;flow+=now;val-=now;
        if(val<=)    break;
    }
    if(val!=flow)    dfn[x]=-;
    return flow;
}

int maxflow(){
    int ans=;
    while(bfs()){
        memset(vis,,sizeof(vis));
        for(int i=;i<=End;++i)    list[i]=head[i];
        int now=dfs(Start,0x7fffffff);
        if(!now)    break;
        ans+=now;
    }
    return ans;
}

int cnt;
bool mst[maxn+maxm+];
int c[maxn][maxm];
int tot[maxm];

int main(){
    int m=read(),n=read();End=n+m+;
    string S;
    for(int i=;i<=m;++i){
        int x=read();
        cnt+=x;
        add(Start,i,x);
        getline(cin,S);
        int len=S.length();
        for(int j=;j<len;++j){
            if(S[j]==' ')    continue;
            x=;
            while(isdigit(S[j])){
                x=x*+S[j]-'';
                j++;
            }
            c[i][++tot[i]]=x;
        }
        for(int j=;j<=tot[i];++j)    add(i,c[i][j]+m,0x7fffffff);
    }
    for(int i=;i<=n;++i){
        int x=read();
        add(i+m,End,x);
    }
    int ans=maxflow();
    for(int i=;i<=m;++i)
        if(dis[i]^)    printf("%d ",i);
    printf("\n");
    for(int i=;i<=n;++i)
        if(dis[i+m]^)    printf("%d ",i);
    printf("\n%d",cnt-ans);
    return ;
}