Luogu P2458 [SDOI2006]保安站岗【树形Dp】

题目描述

五一来临，某地下超市为了便于疏通和指挥密集的人员和车辆，以免造成超市内的混乱和拥挤，准备临时从外单位调用部分保安来维持交通秩序。

已知整个地下超市的所有通道呈一棵树的形状；某些通道之间可以互相望见。总经理要求所有通道的每个端点（树的顶点）都要有人全天候看守，在不同的通道端点安排保安所需的费用不同。

一个保安一旦站在某个通道的其中一个端点，那么他除了能看守住他所站的那个端点，也能看到这个通道的另一个端点，所以一个保安可能同时能看守住多个端点（树的结点），因此没有必要在每个通道的端点都安排保安。

编程任务：

请你帮助超市经理策划安排，在能看守全部通道端点的前提下，使得花费的经费最少。

输入输出格式

输入格式：

第1行 n，表示树中结点的数目。

第2行至第n+1行，每行描述每个通道端点的信息，依次为：该结点标号i（0<i<=n），在该结点安置保安所需的经费k（<=10000），该边的儿子数m，接下来m个数，分别是这个节点的m个儿子的标号r1，r2，...，rm。

对于一个n（0 < n <= 1500）个结点的树，结点标号在1到n之间，且标号不重复。

输出格式：

最少的经费。

如右图的输入数据示例

输出数据示例：

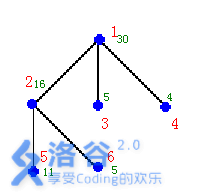
输入输出样例

输入样例#1：

6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0

输出样例#1：

25

说明

样例说明：在结点2，3，4安置3个保安能看守所有的6个结点，需要的经费最小：25

Sol

背景和战略游戏是一样的，但是战略游戏求的是树上的最小点覆盖，可以用树形dp，也可以用二分图的一个定理。也就是说放置士兵的个数。

但本题求的是最小权值，而且稍有不同的是，本题望的是点，战略游戏望边。

但是不管怎么样，它还是在树上啊！树形dp能搞过。

我们冷静分析可知：一个节点有三种情况

0：当前没有被看，将来会被父节点看

（ 由于树形dp是从下往上传递信息的 ）

1：当前被看，且此处有保安

2：当前被看，但 是因为儿子处有保安。

则状态显然: f[x][0/1/2] 表示以x为根的子树的不同情况下所需的最小权值。

对于情况0，f [x] [0] + =sigma -> min( f[y][2],f[y][1] )  只要儿子节点被看就好。

对于情况1，f [x] [1] +=sigma  -> min ( f[y][2],f[y][1],f[y][0] ) +val[x]

对于情况2，f [x] [2] +=sigma  -> min ( f[y][2],f[y][1] ) 但当前节点是被看的，则必须满足有一个儿子的f[y][1]小于f[y][2]，但当没有这个条件满足时，也需要一个f[y][1]，我们可以求出所有儿子的这两个值之差的最小值，取一个f[y][1]。

最后结果即为 max ( f[root][1],f[root][2] ）

注：这道题默认1是根节点，但题面（貌似）没有给出明确的暗示，所有最好还是养成找根节点的习惯。

code

 #include<cstdio>
 #include<algorithm>
 #include<cmath>

 using namespace std;
 typedef long long ll;

 int n,tot;
 int head[],f[][];

 struct node{
     int to,next;
 }edge[];

 void add(int x,int y)
 {
     edge[++tot].to=y;
     edge[tot].next=head[x];
     head[x]=tot;
 }

 void TreeDP(int x,int fa)
 {
     int cha=0x7f7f7f7f,cnt=;
     for(int i=head[x];i;i=edge[i].next)
     {
         int y=edge[i].to;
         if(y==fa) continue;
         TreeDP(y,x);
         f[x][]+=min(f[y][],f[y][]);
         f[x][]+=min(min(f[y][],f[y][]),f[y][]);
         /*if(f[y][1]<f[y][2]) f[x][2]+=f[y][1],flag=true;
         else
         {
             if(flag) f[x][2]+=f[y][2];
             else
              if(fabs(f[y][1]-f[y][2])<min_cha)
               min_cha=fabs(f[y][1]-f[y][2]),jian=f[y][2],jia=f[y][1],f[x][2]+=f[y][2];
              else f[x][2]+=f[y][2];
         }
     }
     if(!flag) f[x][2]=f[x][2]-jian+jia;*///我写的初始版本，但是太丑了QAQ
         if(f[y][]<f[y][]) cnt++;
         else cha=min(cha,f[y][]-f[y][]);
         f[x][]+=min(f[y][],f[y][]);
         }
         if(cnt==) f[x][]+=cha;
 }

 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++)
     {
         int p,k,u,m;
         scanf("%d%d%d",&p,&k,&m);
         f[p][]=k;//注意这句！我被坑了好久！不是f[i][1]=k!
         for(int i=;i<=m;i++)
         {
             scanf("%d",&u);
             add(p,u);//由于没有暗示本题有明确的父子关系，所以还是连双向边的好
             add(u,p);
         }
     }
     TreeDP(,);//dfs传两个参数，一个是当前节点，一个是当前节点的父节点，是个好习惯，可以在后来的判断中防止死循环以及奇怪的MLE！
     printf("%d",min(f[][],f[][]));
     return ;
 }

小结：本题是进阶的树形dp，只要把情况仔细梳理认真分类讨论就ok了！