软件工程作业-(third)
1.选题目(1) 最大连续子数组和(最大子段和)
问题:给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20
2.程序设计和代码
2.1GITHUB代码地址https://github.com/Lpofeng/find_max_add.git
2.2程序流程图
此次采用判定/条件覆盖
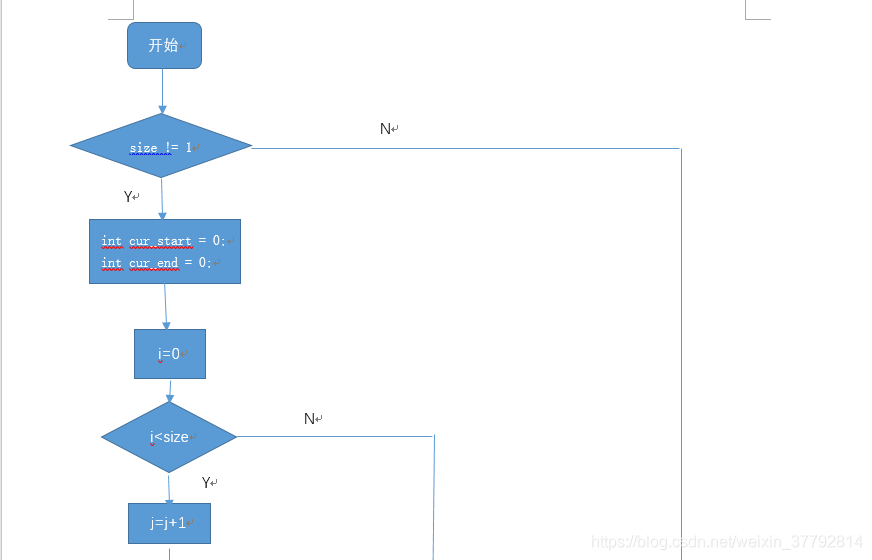
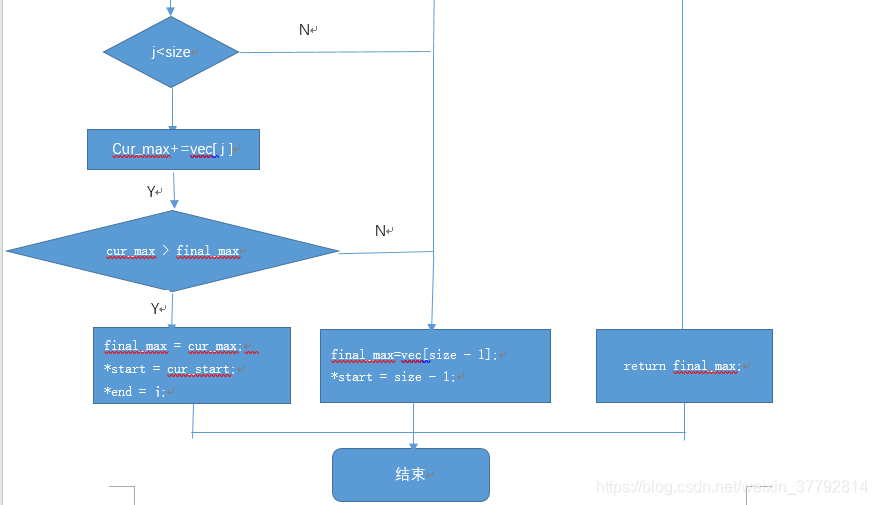
2.3核心代码
int find_max_add(vector<int> vec, const int size, int* start, int* end)
{
if (size == 0)
return -100;
int final_max = vec[0]>0?vec[0]:0;
if (size != 1) {
int cur_start = 0;
int cur_end = 0;
for (int i = 0; i < size; ++i)
{
int cur_max = vec[i];
cur_start = i;
for (int j = i + 1; j < size; ++j)
{
cur_max += vec[j];
if (cur_max > final_max)
{
final_max = cur_max;
*start = cur_start;
*end = j;
}
}
}
if (final_max < vec[size - 1])
{
final_max=vec[size - 1];
*start = size - 1;
}
}
return final_max;
}
3.测试代码
TEST_METHOD(TestMethod1)
{
int s = 0;
int e = 0;
vector<int> v = { -2,-1,-3,5};
Assert::AreEqual(5,find_max_add(v, 4, &s, &e));
}
TEST_METHOD(TestMethod2)
{
int s = 0;
int e = 0;
vector<int> v = {-3,-1,0,5,99,-150 };
Assert::AreEqual(104, find_max_add(v, 6, &s, &e));
}
TEST_METHOD(TestMethod3)
{
int s = 0;
int e = 0;
vector<int> v = { -20,-1,30,5,-10,33,-49,-13 };
Assert::AreEqual(58, find_max_add(v, 8, &s, &e));
}
TEST_METHOD(TestMethod4)
{
int s = 0;
int e = 0;
vector<int> v = { -41,-28,-0,-3,-5,-33,-44,0 };
Assert::AreEqual(0, find_max_add(v, 8, &s, &e));
}
4样例测试结果
源代码测试
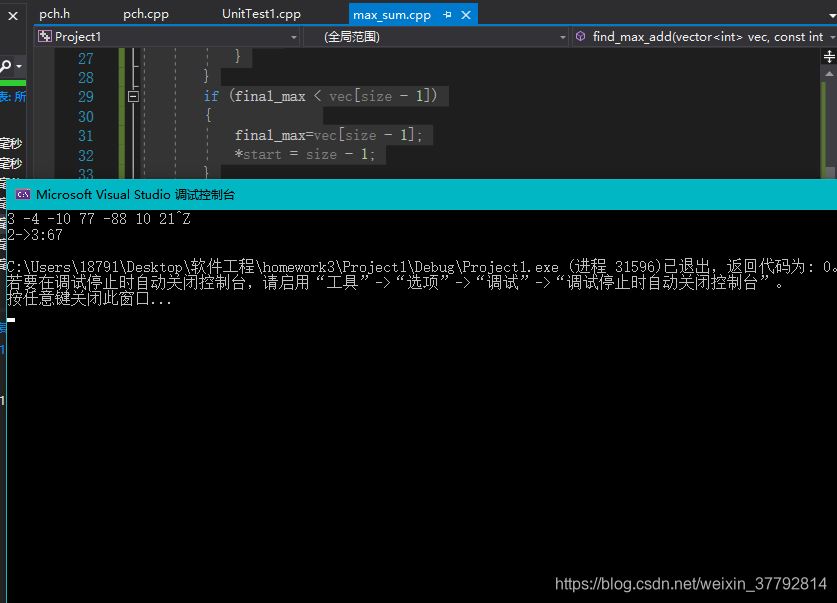
测试代码
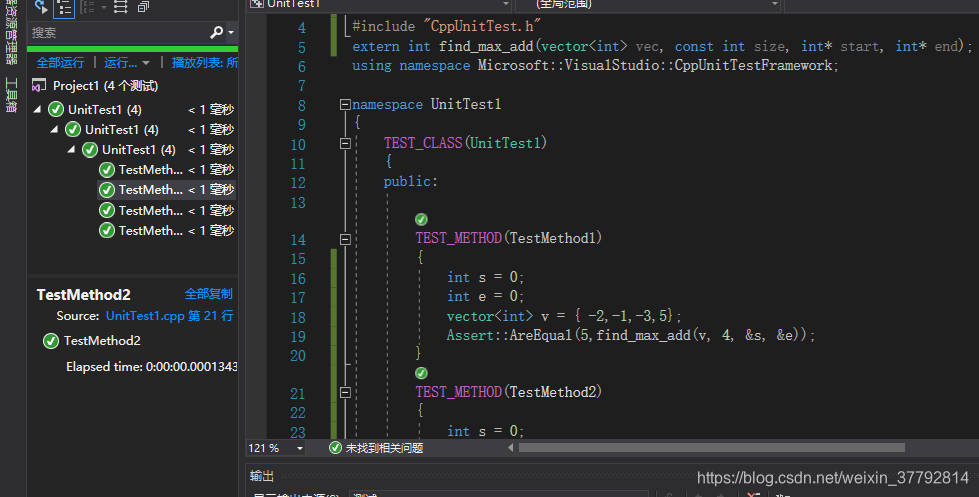
软件工程作业-(third)的更多相关文章
- 软件工程作业 - word count
(编程和软件工程作业系列) 实践最简单的项目:WC 实践是理论的基础和验证标准,希望读者贯彻“做中学”的思想,动手实现下面的项目,并和别人的成绩相比较,分析产生差距的原因. 1. 实现一个简单而完整的 ...
- 第一次软件工程作业——html制作一份简单的个人简历
源码链接(码云):https://gitee.com/yongliuli/codes/eavjr7lxotb85s0icnq1z68 简历效果图展示: 代码展示: 添加背景音乐的方法: 在<he ...
- 第一次软件工程作业(One who wants to wear the crown, Bears the crown.)
回顾你过去将近3年的学习经历 1.当初报考的时候,是真正的喜欢计算机这个专业吗? 报考时对于计算机专业只能说不讨厌,也可以认为对其没有任何的感觉. 有一个比我自己还注意我未来的老妈,我的报考只能通过一 ...
- 软件工程作业 - Week 1
构建之法读后疑问: 初步的完成构建程序设计思路之后实现过程中发现了问题或者可以优化的地方是立马就改进还是完成之后按照步骤统一进行优化. 覆盖性测试,针对一些永远用不到只是用来预防极为极端的情况下,例如 ...
- 第一次软件工程作业补充plus
一.代码的coding地址:coding地址. 二.<构建之法>读后问题以及感言(补充): 1.对于7.3MSF团队模型,7.2.6保持敏捷,预期和适应变化,中的"我们是预期变化 ...
- 软件工程作业——Word Counter
github地址 https://github.com/Pryriat/Word_Counter 项目说明 wc.exe 是一个常见的工具,它能统计文本文件的字符数.单词数和行数.这个项目要求写一个命 ...
- 软件工程作业0——The Road Not Taken
目录 第一部分:结缘计算机 缘起 四顾 思考 第二部分:在计算机系里学习 挑战 落差 第三部分:未来规划 向前 未来四个月的软工课 项目 内容 这个作业属于 2020春季计算机学院软件工程(罗杰 任健 ...
- 现代软件工程作业 第二章 Github的使用
Github的使用 创建团队 Github首页点击Create Orginazation,出现如下界面: 填写相关信息,邀请团队成员: 点击确认,创建团队完成,界面如下: 创建新的版本库 点击Crea ...
- 现代软件工程作业-- GitHub的学习
1.注册github账号: 2.在github上面新建一个名为HelloWord的项目: 3.将本组的其他成员纳入到HelloWorld中: 4.复制远端仓库的地址: 5.在本地的git bash中使 ...
- 现代软件工程作业 第二章 学习github笔记
在网上大量资料的辅助下,学习了github的基本使用方法,尝试了一些常见的命令.为了便于记忆总结了自己的学习内容. 1.首先需要在github的官网上注册一个帐号,并新建一个repository,选这 ...
随机推荐
- bzoj 2002 : [Hnoi2010]Bounce 弹飞绵羊 (LCT)
链接:https://www.lydsy.com/JudgeOnline/problem.php?id=2002 题面: 2002: [Hnoi2010]Bounce 弹飞绵羊 Time Limit: ...
- TortoiseSVN版本管理的注意点
@2019-04-18 [小记] 1.强烈建议以项目(功能区别较大(单.双机做两个版本))为区别单独版本管理,这样可保证工程的延续性(能更好的使用更新.提交等功能)及避免后期提交时的混乱(.svn信息 ...
- fastclick原理剖析及其用法
移动端点击延迟事件 移动端浏览器在派发点击事件的时候,通常会出现300ms左右的延迟. 原因: 移动端的双击会缩放导致click判断延迟.这是为了检查用户是否在做双击.为了能够立即响应用户的点击事件, ...
- 堆以及一些用法 QWQ这是写得最认真的板子题
最近一直在学图论,然后吧,由于学的东西实在是太多太杂了,加上蒟蒻本蒻又经常颓,所以落了好多好多板子题的整理没写啊嘤嘤嘤,不过把这些东西学的差不多了,再一块写个整理,其实感觉还不错?????也算是很神奇 ...
- 【洛谷P1659】啦啦队排练
题目大意:给定一个长度为 N 的字符串,求前 K 个长度为奇数的回文子串的长度的乘积是多少. 题解:利用回文自动机,将所有长度的回文串和个数求出来,按照长度排序进行模拟即可. 代码如下 // luog ...
- 20175221 MyCP(课下作业,必做)
MyCP(课下作业,必做) 任务详情 编写MyCP.java 实现类似Linux下cp XXX1 XXX2的功能,要求MyCP支持两个参数: - java MyCP -tx XXX1.txt XXX2 ...
- MAC上有哪些优秀的日常软件| 入门级Mac OS 用户必备软件
本文整理的网友反馈的MAC上有哪些优秀的日常软件+入门级Mac OS 用户必备软件,感兴趣的朋友可以看看,下载下来试用一样便知实不实用.如有更好的推荐,欢迎留言. MAC上有哪些优秀的日常软件 Tim ...
- 将图片转为base64
DEMO: <input type="file" id="file" multiple="multiple"> <div ...
- 第十一节:WebApi的版本管理的几种方式
一. 背景和方案 1. 多版本管理的概念 Android .IOS等 App 存在着多版本客户端共存的问题:App 最新版已经升级到了5.0 了,但是有的用户手机上还运行着 4.8.3.9 甚至2.2 ...
- jQuery 条件搜索查询 实时取值 升降序排序
一.鼠标点击获取搜索条件中的被选中的值 创建方法 getAttrValue() 方法,每次的 .click 都要调用 function getAttrValue(){} 例如,把选中的值给到属性 ...
