Floyd判断环算法总结

Floyd判断环算法

全名Floyd’s cycle detection Algorithm, 又叫龟兔赛跑算法（Floyd's Tortoise and Hare），常用于链表、数组转化成链表的题目中。

情景介绍

我们将设置两个指针：slow和fast。slow一次走一格，fast一次走两格。

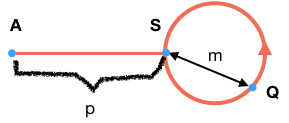
p :环之前的距离

m：S和Q之间的步数

A：链表起点

S：循环起点

Q：初次相遇点

L ：环的长度

k ：环数

判断是否有环

若在某一时刻slow和fast相遇，则存在环（又可叫Two Pointers 方法）

[1] slow_step = p + L * k1 + m;

[2] fast_step = 2 * slow_step = p + L * k2 + m;

[2] - [1] = [1] = L * (k2 - k1) 由此可知slow走过的步数是L的倍数 => p + m是L的倍数

找循环起点S

fast从Q继续走，slow从A重走，当二者再次相遇，此时slow必然刚好走到循环起点S，fast也必然走到循环起点S。

证明：

slow_step = p

fast_step = L - m + L * k3

fast_step - slow_step = L - m - p + L * k3= L * k4 (因为 p + m 是L的倍数)

计算循环长度L

[1]当slow和fast初次相遇后

标记相遇的值，new一个新指针重新绕环走，计算走过的步数，当再次到达相遇值，走过的步数即为L。

[2]找到S后

进入循环，当再次到达S时，所走的步数即为L。

算法复杂度：

T～N，S～1

相关题目：

141. Linked List Cycle

142. Linked List Cycle II

202. Happy Number

287. Find the Duplicate Number

Tips：

当需要判断链表或者数组关于环/是否有环/找循环起始点/循环长度，或者需要利用数组的index和val值时，考虑Floyd算法。