2022-10-09：我们给出了一个（轴对齐的）二维矩形列表 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2]，其中（x1，y1）是矩形 i 左下角的坐

2022-10-09：我们给出了一个（轴对齐的）二维矩形列表 rectangles 。
对于 rectangle[i] = [x1, y1, x2, y2]，其中（x1，y1）是矩形 i 左下角的坐标
(xi1, yi1) 是该矩形 左下角 的坐标， (xi2, yi2) 是该矩形 右上角 的坐标。
计算平面中所有 rectangles 所覆盖的 总面积 。
任何被两个或多个矩形覆盖的区域应只计算 一次 。
返回 总面积 。因为答案可能太大，返回 10^9 + 7 的 模 。
输入：rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]。
输出：6。

答案2022-10-09：

线段树模板题。一个矩形两个事件。这道题用了树结构，对于rust有点复杂，用了Rc<RefCell>的数据类型。
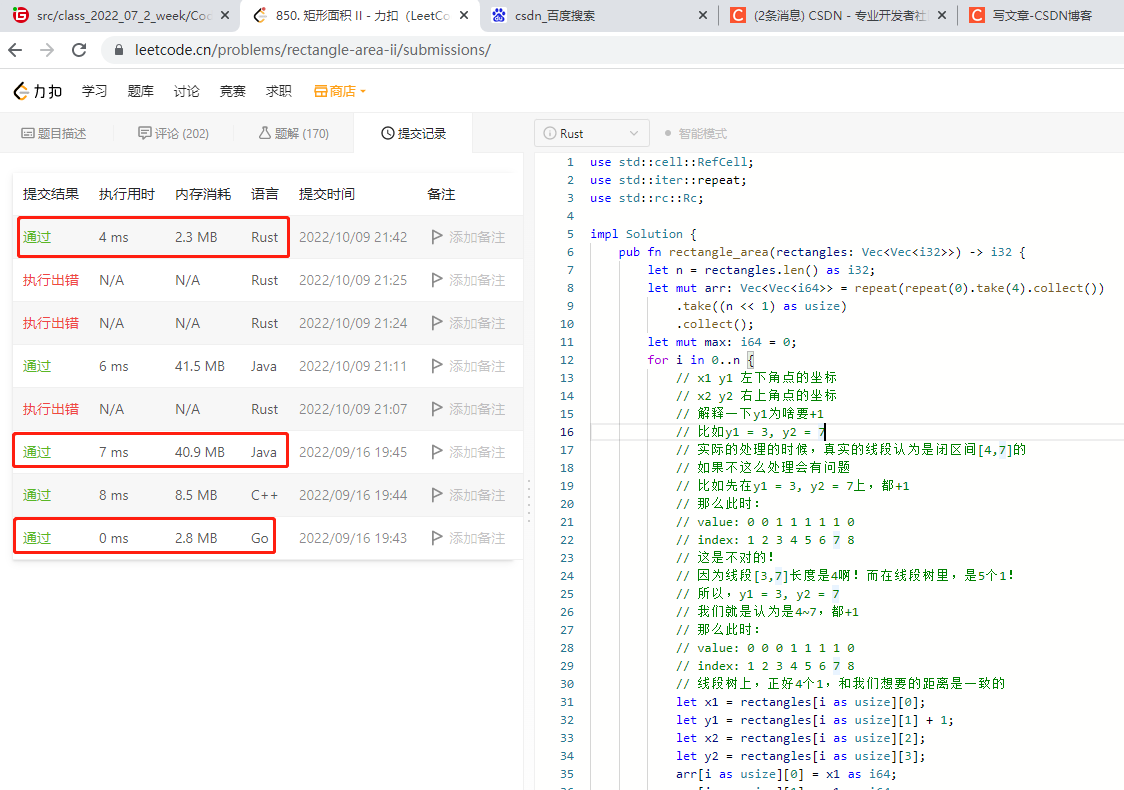
力扣850上测试，rust语言占用内存最低，go语言占用内存略高于rust，但运行速度最快。
不管怎么说，rust和go都是要优于java的。用java的人们，你们赶紧换语言，java过时了。
java，go，rust运行情况见截图。

代码用rust编写。代码如下：

use std::cell::RefCell;
use std::iter::repeat;
use std::rc::Rc;

impl Solution {
    pub fn rectangle_area(rectangles: Vec<Vec<i32>>) -> i32 {
        let n = rectangles.len() as i32;
        let mut arr: Vec<Vec<i64>> = repeat(repeat(0).take(4).collect())
            .take((n << 1) as usize)
            .collect();
        let mut max: i64 = 0;
        for i in 0..n {
            // x1 y1 左下角点的坐标
            // x2 y2 右上角点的坐标
            // 解释一下y1为啥要+1
            // 比如y1 = 3, y2 = 7
            // 实际的处理的时候，真实的线段认为是闭区间[4,7]的
            // 如果不这么处理会有问题
            // 比如先在y1 = 3, y2 = 7上，都+1
            // 那么此时：
            // value: 0 0 1 1 1 1 1 0
            // index: 1 2 3 4 5 6 7 8
            // 这是不对的！
            // 因为线段[3,7]长度是4啊！而在线段树里，是5个1！
            // 所以，y1 = 3, y2 = 7
            // 我们就是认为是4~7，都+1
            // 那么此时：
            // value: 0 0 0 1 1 1 1 0
            // index: 1 2 3 4 5 6 7 8
            // 线段树上，正好4个1，和我们想要的距离是一致的
            let x1 = rectangles[i as usize][0];
            let y1 = rectangles[i as usize][1] + 1;
            let x2 = rectangles[i as usize][2];
            let y2 = rectangles[i as usize][3];
            arr[i as usize][0] = x1 as i64;
            arr[i as usize][1] = y1 as i64;
            arr[i as usize][2] = y2 as i64;
            arr[i as usize][3] = 1;
            arr[(i + n) as usize][0] = x2 as i64;
            arr[(i + n) as usize][1] = y1 as i64;
            arr[(i + n) as usize][2] = y2 as i64;
            arr[(i + n) as usize][3] = -1;
            max = get_max(max, y2 as i64);
        }
        return cover_area(&mut arr, n << 1, max);
    }
}

fn get_max<T: Clone + Copy + std::cmp::PartialOrd>(a: T, b: T) -> T {
    if a > b {
        a
    } else {
        b
    }
}

fn cover_area(arr: &mut Vec<Vec<i64>>, n: i32, max: i64) -> i32 {
    // 所有的事件，都在arr里
    // [x, y1, y2, +1/-1]
    // 早 -> 晚
    //Arrays.sort(arr, 0, n, (a, b) -> a[0] <= b[0] ? -1 : 1);
    arr[0..n as usize].sort_by(|a, b| {
        if a[0] < b[0] {
            std::cmp::Ordering::Less
        } else {
            std::cmp::Ordering::Greater
        }
    });

    // max y的值，可能的最大值，非常大也支持！
    let mut dst = DynamicSegmentTree::new(max);
    let mut pre_x: i64 = 0;
    let mut ans: i64 = 0;
    for i in 0..n {
        // dst.query() : 开点线段树告诉你！y方向真实的长度！
        ans += dst.query() * (arr[i as usize][0] - pre_x);
        ans %= 1000000007;
        pre_x = arr[i as usize][0];
        dst.add(arr[i as usize][1], arr[i as usize][2], arr[i as usize][3]);
    }
    return ans as i32;
}

struct Node {
    cover: i64,
    len: i64,
    left: Option<Rc<RefCell<Node>>>,
    right: Option<Rc<RefCell<Node>>>,
}

impl Node {
    fn new() -> Self {
        Self {
            cover: 0,
            len: 0,
            left: Option::None,
            right: Option::None,
        }
    }
}
struct DynamicSegmentTree {
    root: Rc<RefCell<Node>>,
    size: i64,
}

impl DynamicSegmentTree {
    fn new(max: i64) -> Self {
        Self {
            root: Rc::new(RefCell::new(Node::new())),
            size: max,
        }
    }
    pub fn add(&mut self, ll: i64, rr: i64, cover: i64) {
        self.add0(Rc::clone(&self.root), 1, self.size, ll, rr, cover);
    }

    fn add0(&mut self, cur: Rc<RefCell<Node>>, l: i64, r: i64, ll: i64, rr: i64, cover: i64) {
        if ll <= l && rr >= r {
            cur.as_ref().borrow_mut().cover += cover;
        } else {
            if cur.as_ref().borrow().left.is_none() {
                cur.as_ref().borrow_mut().left = Some(Rc::new(RefCell::new(Node::new())));
            }
            if cur.as_ref().borrow().right.is_none() {
                cur.as_ref().borrow_mut().right = Some(Rc::new(RefCell::new(Node::new())));
            }
            let m: i64 = l + ((r - l) >> 1);
            if ll <= m {
                self.add0(
                    Rc::clone(&cur.as_ref().borrow().left.as_ref().unwrap()),
                    l,
                    m,
                    ll,
                    rr,
                    cover,
                );
            }
            if rr > m {
                self.add0(
                    Rc::clone(&cur.as_ref().borrow().right.as_ref().unwrap()),
                    m + 1,
                    r,
                    ll,
                    rr,
                    cover,
                );
            }
        }
        self.push_up(cur, l, r);
    }

    fn push_up(&mut self, cur: Rc<RefCell<Node>>, l: i64, r: i64) {
        if cur.as_ref().borrow().cover > 0 {
            cur.as_ref().borrow_mut().len = r - l + 1;
        } else {
            cur.as_ref().borrow_mut().len = if !cur.as_ref().borrow().left.is_none() {
                cur.as_ref()
                    .borrow_mut()
                    .left
                    .as_mut()
                    .unwrap()
                    .as_ref()
                    .borrow()
                    .len
            } else {
                0
            } + if !cur.as_ref().borrow().right.is_none() {
                cur.as_ref()
                    .borrow_mut()
                    .right
                    .as_mut()
                    .unwrap()
                    .as_ref()
                    .borrow()
                    .len
            } else {
                0
            };
        }
    }

    pub fn query(&mut self) -> i64 {
        return self.root.as_ref().borrow().len;
    }
}

fn main() {
    let rectangles = vec![vec![0, 0, 2, 2], vec![1, 0, 2, 3], vec![1, 0, 3, 1]];
    let ans = Solution::rectangle_area(rectangles);
    println!("ans = {:?}", ans);
}

struct Solution {}

执行结果如下：

---

左神java代码