B树-插入

B树系列文章

1. B树-介绍

2. B树-查找

3. B树-插入

4. B树-删除

插入

根据B树的以下两个特性

• 每一个结点最多有m个子结点
• 有k个子结点的非叶子结点拥有 k − 1 个键

可以得出，B树每个结点存放键的数量是有上限的是m-1，因此插入操作可能导致结点“溢出”。

插入操作的重点和难点在于结点“溢出”后的再平衡操作

假设有一棵3阶B树，如下图所示。

 

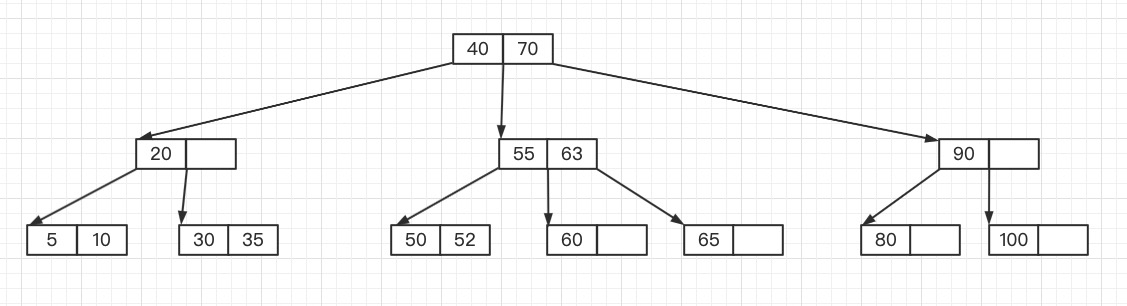
通过给这棵3阶B树插入键值53，来分析B树插入键值的过程。

首先，参考查找的步骤，最终定位到53应该插入到Node21结点的最后

但是这是一个3阶B树，每个结点拥有键的最大数量为2，因此插入53会导致Node21"溢出"

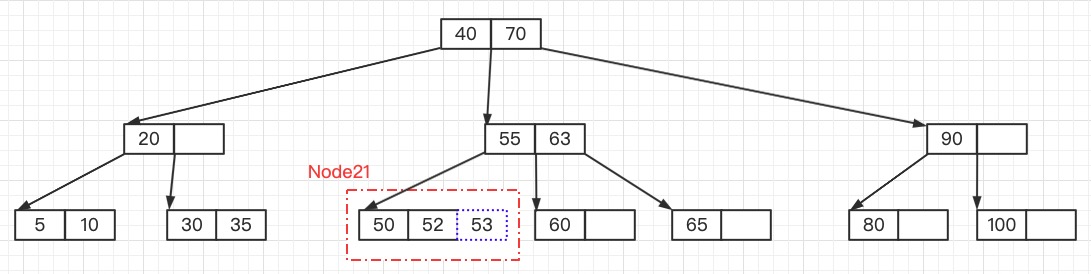
由于Node21结点“溢出”，需要对Node21进行拆分，拆分方法如下

• 从该结点的原有键和新的键中选择出中位数，这个中位数作为分隔值
• 小于这一中位数的键放入左边结点，大于这一中位数的键放入右边结点，中位数作为分隔值。
• 分隔值被插入到父结点中，这可能会造成父结点分裂，分裂父结点时可能又会使它的父结点分裂，以此类推。如果没有父结点（这一结点是根结点），就创建一个新的根结点（增加了树的高度）。

下图是对Node21进行拆分的结果，Node21分裂成两个新的结点和分隔值53，53需要插入父结点中

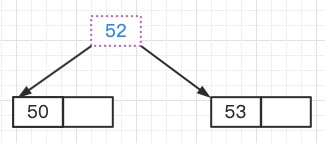
将分隔值插入父结点中，形成Node2结点，原来的Node21结点被拆分为新的Node21和Node22结点

可以看出来，此时Node2结点键的数量达到了阶数，即达到“溢出”条件了

因此，需要继续对Node2进行拆分

对Node2进行拆分，中间值55提升到root结点，原来的Node2结点拆分成Node2和Node3两个新结点

同样的，此时root结点也“溢出”了，需要对root结点进行拆分

对root结点的拆分，最终造成B树高度的增加

对根结点进行拆分，55被提升，需要创建新的根结点存放键55，键值40和70分别构成新的两个儿子结点，分别是Node1和Node12

此时B数重新平衡了。

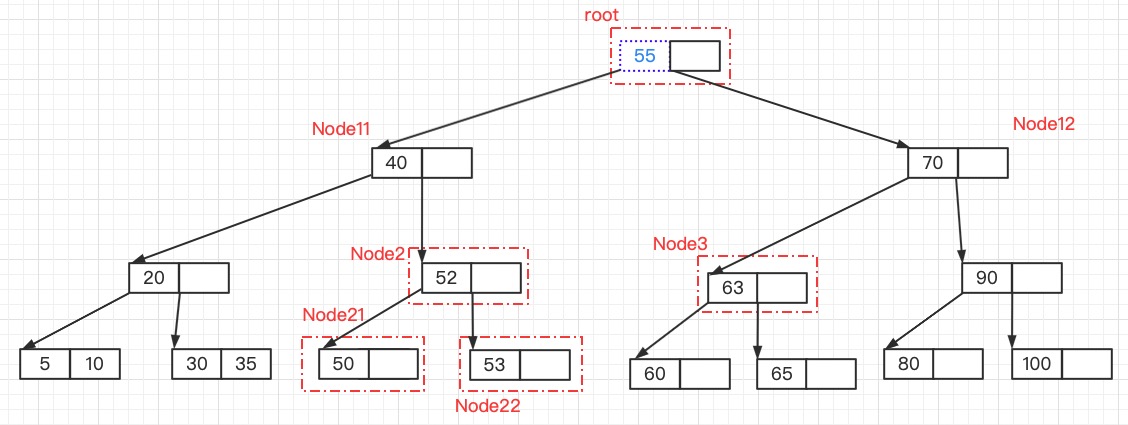
这里总结下

所有的插入都从根结点开始。要插入一个新的键，首先搜索这棵树找到新键应该被添加到的对应结点。将新键插入到这一结点中的步骤如下：

如果结点拥有的键数量小于最大值，那么有空间容纳新的键。将新键插入到这一结点，且保持结点中键有序。

否则的话这一结点已经满了，将它平均地拆分成两个结点：

从该结点的原有键和新的键中选择出中位数

小于这一中位数的键放入左边结点，大于这一中位数的键放入右边结点，中位数作为分隔值。

分隔值被插入到父结点中，这可能会造成父结点分裂，分裂父结点时可能又会使它的父结点分裂，以此类推。如果没有父结点（这一结点是根结点），就创建一个新的根结点（增加了树的高度）。

这里是插入的代码

/**
* 插入key
* 时间复杂度为O(logn)
**/
func (bTreeNode *BTreeNode) intert(key int, m int) ([]*BTreeNode, int) {
    // 找到第一个不比key小的，注意leaf的数量比key数量多1
    idx := 0
    for idx < bTreeNode.keyNum && key > bTreeNode.keyList[idx] {
        idx++
    }

    // BTreeNode已有该key
    if idx < bTreeNode.keyNum && bTreeNode.keyList[idx] == key {
        return nil, 0
    }

    if bTreeNode.isLeaf { // 叶子结点
        // idx及idx后面元素往后移动
        if idx < m-1 {
            copy(bTreeNode.keyList[idx+1:], bTreeNode.keyList[idx:])
        }
        bTreeNode.keyList[idx] = key
        bTreeNode.keyNum += 1
    } else { // 非叶子结点
        // 判断结点是否要满了
        // 先往上提
        children, midKey := bTreeNode.leafList[idx].intert(key, m)
        if children != nil {
            // idx是midKey的插入位置,idx后面元素往后移动
            if idx < m-1 {
                copy(bTreeNode.keyList[idx+1:], bTreeNode.keyList[idx:])
                copy(bTreeNode.leafList[idx+2:], bTreeNode.leafList[idx+1:])
            }
            bTreeNode.keyList[idx] = midKey
            bTreeNode.leafList[idx] = children[0]
            bTreeNode.leafList[idx+1] = children[1]
            bTreeNode.keyNum += 1
        }
    }

    if bTreeNode.keyNum == m { // 节点key数量超了
        // 从中间将该结点一分为2
        mid := bTreeNode.keyNum / 2
        midKey := bTreeNode.keyList[mid]

        // 左儿子
        leftNode := createNode(m, mid, bTreeNode.isLeaf)
        copy(leftNode.keyList, bTreeNode.keyList[:mid])
        copy(leftNode.leafList, bTreeNode.leafList[:mid+1])

        // 右边儿子
        rightNode := createNode(m, m-mid-1, bTreeNode.isLeaf)
        copy(rightNode.keyList, bTreeNode.keyList[mid+1:])
        copy(rightNode.leafList, bTreeNode.leafList[mid+1:])

        return []*BTreeNode{leftNode, rightNode}, midKey
    }
    return nil, 0
}

/** 插入key
* 时间复杂度O(logn)
**/
func (bTree *BTree) Insert(key int) {
    children, midKey := bTree.root.intert(key, bTree.m)
    if children != nil {
        root := createNode(bTree.m, 1, false)
        root.keyList[0] = midKey
        root.leafList[0] = children[0]
        root.leafList[1] = children[1]
        bTree.root = root
    }
}