机器学习进阶-直方图与傅里叶变换-傅里叶变换(高低通滤波) 1.cv2.dft(进行傅里叶变化) 2.np.fft.fftshift(将低频移动到图像的中心) 3.cv2.magnitude(计算矩阵的加和平方根) 4.np.fft.ifftshift(将低频和高频移动到原来位置) 5.cv2.idft(傅里叶逆变换)

1. cv2.dft(img, cv2.DFT_COMPLEX_OUTPUT) 进行傅里叶变化

参数说明: img表示输入的图片， cv2.DFT_COMPLEX_OUTPUT表示进行傅里叶变化的方法

2. np.fft.fftshift(img)  将图像中的低频部分移动到图像的中心

参数说明：img表示输入的图片

3. cv2.magnitude(x, y) 将sqrt(x^2 + y^2) 计算矩阵维度的平方根

参数说明：需要进行x和y平方的数

4.np.fft.ifftshift(img) # 进图像的低频和高频部分移动到图像原来的位置

参数说明：img表示输入的图片

5.cv2.idft(img) # 进行傅里叶的逆变化

参数说明：img表示经过傅里叶变化后的图片

傅里叶变化：将图像从空间域转换为频率域， 下面是傅里叶变化的公式

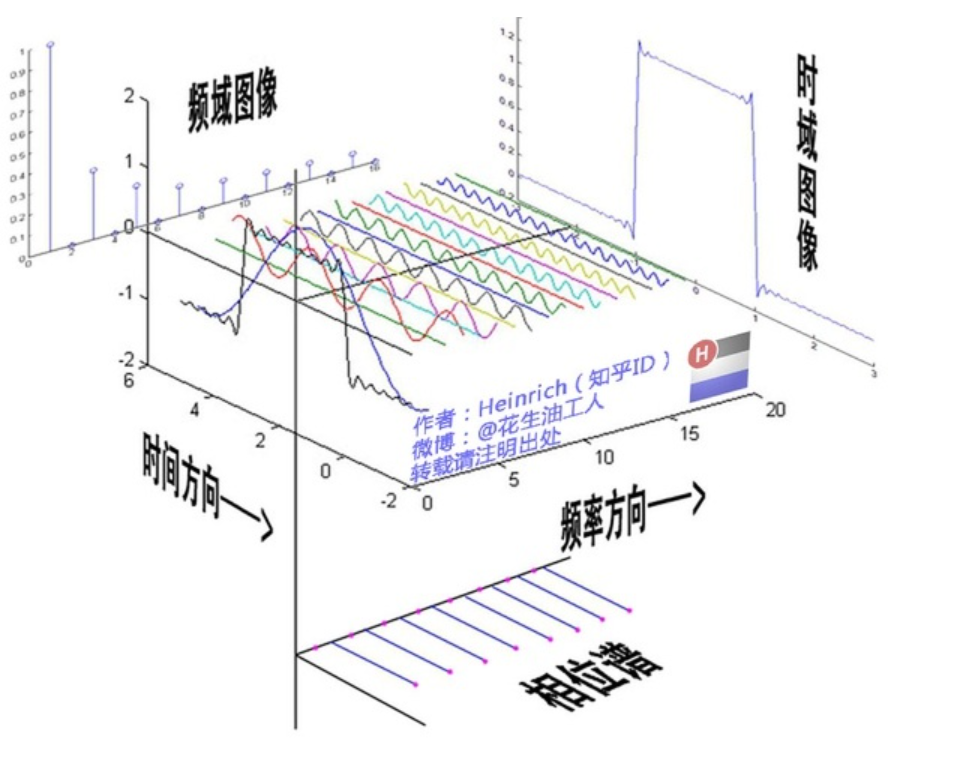
对应于频率的方向，我们可以看出红色那条线的频率最小，蓝色线的频率最大， 高频指变化剧烈的灰度分量，即图像边界的地方, 低频指变换缓慢的灰度分量

构建出的傅里叶变化的图片，将低频移到中间位置， 通常呈现中间亮，周围暗，是因为对于低频而言，波动较大，比如红色那条线，因此呈现亮，对于高频而言，波动较小，比如蓝色那条线，因此呈现暗

代码：

第一步：载入图片

第二步：使用np.float32进行格式转换

第三步：使用cv2.dft进行傅里叶变化

第四步：使用np.fft.shiftfft将低频转移到中间位置

第五步：使用cv2.magnitude将实部和虚部投影到空间域

第六步：进行作图操作

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 第一步读取图片
img = cv2.imread('lena.jpg', 0)

# 第二步：进行float32形式转换
float32_img = np.float32(img)

# 第三步: 使用cv2.dft进行傅里叶变化
dft_img = cv2.dft(float32_img, flags=cv2.DFT_COMPLEX_OUTPUT)

# 第四步：使用np.fft.shiftfft()将变化后的图像的低频转移到中心位置
dft_img_ce = np.fft.fftshift(dft_img)

# 第五步：使用cv2.magnitude将实部和虚部转换为实部，乘以20是为了使得结果更大
img_dft = 20 * np.log(cv2.magnitude(dft_img_ce[:, :, 0], dft_img_ce[:, :, 1]))

# 第六步：进行画图操作
plt.subplot(121)
plt.imshow(img, cmap='gray')
plt.subplot(122)
plt.imshow(img_dft, cmap='gray')
plt.show()

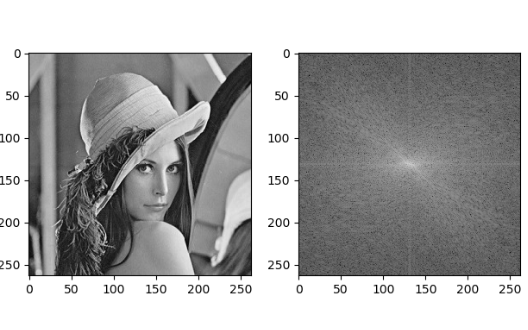
2.只保留低频，即进行低通滤波，因为高频表示是一些细节，即图像的轮廓和边缘，失去了高频部分，图像就容易变得模糊

代码：

第一步：读取图片

第二步：np.float32进行类型转换

第三步：使用cv2.dft进行傅里叶变化

第四步：使用np.fft.fftshift 将低频部分转换到图像的中心

第五步：构造掩模，使得掩模的中心位置为1，边缘位置为0

第六步：将掩模与傅里叶变换后的图像结合，只保留中心部分的低频位置

第七步：使用np.fft.ifftshift将低频部分转移回图像的原先位置

第八步：使用cv2.idft进行傅里叶的反转换

第九步：使用cv2.magnitude将图像的实部和虚部转换为空间域内

第十步：进行作图操作

# 使用掩模只保留低通

# 第一步读入图片
img = cv2.imread('lena.jpg', 0)
# 第二步：进行数据类型转换
img_float = np.float32(img)
# 第三步：使用cv2.dft进行傅里叶变化
dft = cv2.dft(img_float, flags=cv2.DFT_COMPLEX_OUTPUT)
# 第四步：使用np.fft.fftshift将低频转移到图像中心
dft_center = np.fft.fftshift(dft)
# 第五步：定义掩模：生成的掩模中间为1周围为0
crow, ccol = int(img.shape[0] / 2), int(img.shape[1] / 2) # 求得图像的中心点位置
mask = np.zeros((img.shape[0], img.shape[1], 2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1

# 第六步：将掩模与傅里叶变化后图像相乘，保留中间部分
mask_img = dft_center * mask

# 第七步：使用np.fft.ifftshift(将低频移动到原来的位置
img_idf = np.fft.ifftshift(mask_img)

# 第八步：使用cv2.idft进行傅里叶的反变化
img_idf = cv2.idft(img_idf)

# 第九步：使用cv2.magnitude转化为空间域内
img_idf = cv2.magnitude(img_idf[:, :, 0], img_idf[:, :, 1])

# 第十步：进行绘图操作
plt.subplot(121)
plt.imshow(img, cmap='gray')
plt.subplot(122)
plt.imshow(img_idf, cmap='gray')
plt.show()

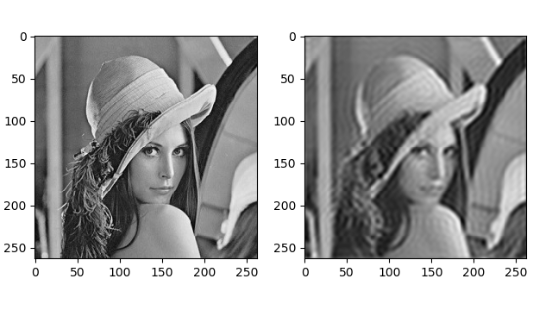
3.只保留图像的高频部分

流程与上面一样，只是构造的掩模是中间为0，边缘为1，然后与傅里叶变化后的图像结合， 保留高频部分，去除低频部分

代码：

# 只保留高频部分
# 使用掩模只保留低通

# 第一步读入图片
img = cv2.imread('lena.jpg', 0)
# 第二步：进行数据类型转换
img_float = np.float32(img)
# 第三步：使用cv2.dft进行傅里叶变化
dft = cv2.dft(img_float, flags=cv2.DFT_COMPLEX_OUTPUT)
# 第四步：使用np.fft.fftshift将低频转移到图像中心
dft_center = np.fft.fftshift(dft)
# 第五步：定义掩模：生成的掩模中间为0周围为1
crow, ccol = int(img.shape[0] / 2), int(img.shape[1] / 2) # 求得图像的中心点位置
mask = np.ones((img.shape[0], img.shape[1], 2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 0

# 第六步：将掩模与傅里叶变化后图像相乘，保留中间部分
mask_img = dft_center * mask

# 第七步：使用np.fft.ifftshift(将低频移动到原来的位置
img_idf = np.fft.ifftshift(mask_img)

# 第八步：使用cv2.idft进行傅里叶的反变化
img_idf = cv2.idft(img_idf)

# 第九步：使用cv2.magnitude转化为空间域内
img_idf = cv2.magnitude(img_idf[:, :, 0], img_idf[:, :, 1])

# 第十步：进行绘图操作
plt.subplot(121)
plt.imshow(img, cmap='gray')
plt.subplot(122)
plt.imshow(img_idf, cmap='gray')
plt.show()

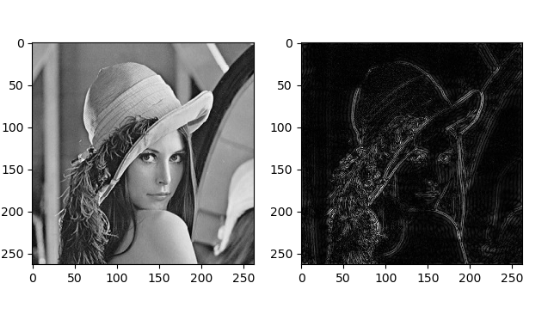
从上图可以看出保留了图像的边缘部分，而其他的信息被去除了