POJ.2774.Long Long Message/SPOJ.1811.LCS(后缀自动机)
题目链接 POJ2774
SPOJ1811 LCS - Longest Common Substring
确实比后缀数组快多了(废话→_→)。
\(Description\)
求两个字符串最长公共子串
\(Solution\)
对串A建立后缀自动机。
A的SAM中包含A的所有子串,且根到每个节点的路径都是A的子串。如果B(的一部分?)匹配到了SAM上的某个节点,那么这便是AB的公共子串。求出这些点的max(len)即可。
用串B在SAM上逐位匹配,如果匹配,就继续沿着匹配边走;
否则,为了匹配当前这位,丢掉B前面一部分,因为fa[p]节点代表的后缀是p所代表后缀的上一个可接受后缀,所以跳fa[p],直到可匹配当前位或到根节点。
注意now的更新方式,如果匹配则+1,否则跳完p后,在p=son[p][c]前用len[p]+1更新now。因为此时p完全匹配了,而len[son[p][c]]是son[p][c]所代表的串的max(len)。(大概是这样吧。。)
感觉这东西好玄学啊。。
//15064K 79MS
//SPOJ:69M 0.04s
#include <cstdio>
#include <cstring>
#include <algorithm>
const int N=250005<<1;//2n
char s[N>>1];
struct Suffix_Automaton
{
int las,tot,son[N][26],fa[N],len[N];
void Insert(int c)
{
int p=las,np=++tot; len[las=np]=len[p]+1;
for(; p&&!son[p][c]; p=fa[p]) son[p][c]=np;
if(!p) fa[np]=1;
else
{
int q=son[p][c];
if(len[q]==len[p]+1) fa[np]=q;
else
{
int nq=++tot; len[nq]=len[p]+1;
memcpy(son[nq],son[q],sizeof son[q]);
fa[nq]=fa[q], fa[q]=fa[np]=nq;
for(; son[p][c]==q; p=fa[p]) son[p][c]=nq;
}
}
}
void Build(char *s)
{
las=tot=1;
for(int i=0,l=strlen(s); i<l; ++i) Insert(s[i]-'a');
}
void Query(char *s)
{
int ans=0;
for(int c,now=0,p=1,i=0,l=strlen(s); i<l; ++i,ans=std::max(ans,now))
if(son[p][c=s[i]-'a']) p=son[p][c], ++now;
else
{
for(; p&&!son[p][c]; p=fa[p]);
if(!p) p=1, now=0;
else now=len[p]+1, p=son[p][c];
// WA: else p=son[p][c], now=len[p];
}
printf("%d",ans);
}
}sam;
int main()
{
scanf("%s",s), sam.Build(s);
scanf("%s",s), sam.Query(s);
return 0;
}
一些有关后缀自动机的东西:
论文。。
构造:
后缀自动机详解(感觉这写的理论好理解)
后缀自动机学习小结(从维护right来写?)
后缀自动机学习总结(从简化状态来写?)
后缀自动机构造过程演示(这个过程演示很好啊)
后缀自动机的构造(没看)
题目:
后缀自动机的性质应用
后缀自动机总结
后缀自动机学习小结(应用理论)
几张SAM的例图:
aabbab
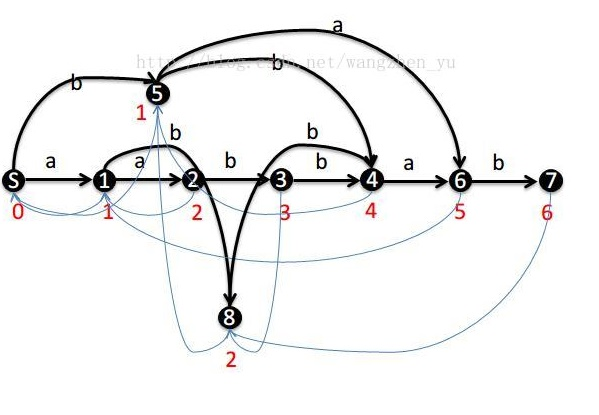
aabb
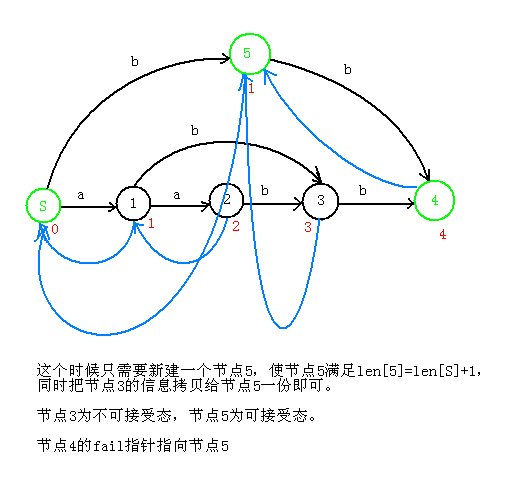
POJ.2774.Long Long Message/SPOJ.1811.LCS(后缀自动机)的更多相关文章
- POJ.2774.Long Long Message/SPOJ.1811.LCS(后缀数组 倍增)
题目链接 POJ2774 SPOJ1811 LCS - Longest Common Substring 比后缀自动机慢好多(废话→_→). \(Description\) 求两个字符串最长公共子串 ...
- SPOJ 1811 LCS [后缀自动机]
题意: 求两个串的最大连续子串 一个串建SAM,另一个串在上面跑 注意如果走了Suffix Link,sum需要更新为t[u].val+1 Suffix Link有点像失配吧,当前状态s走不了了就到S ...
- spoj 1811 LCS - Longest Common Substring (后缀自己主动机)
spoj 1811 LCS - Longest Common Substring 题意: 给出两个串S, T, 求最长公共子串. 限制: |S|, |T| <= 1e5 思路: dp O(n^2 ...
- spoj 1812 lcsII (后缀自动机)
spoj 1812 lcsII (后缀自动机) 题意:求多个串的lcs,最多10个串,每个串最长10w 解题思路:后缀自动机.先建好第一个串的sam,然后后面的串拿上去跑(这个过程同前一题).sam上 ...
- [POJ 2774] Long Long Message 【后缀数组】
题目链接:POJ - 2774 题目分析 题目要求求出两个字符串的最长公共子串,使用后缀数组求解会十分容易. 将两个字符串用特殊字符隔开再连接到一起,求出后缀数组. 可以看出,最长公共子串就是两个字符 ...
- POJ 2774 Long Long Message [ 最长公共子串 后缀数组]
题目:http://poj.org/problem?id=2774 Long Long Message Time Limit: 4000MS Memory Limit: 131072K Total ...
- ●POJ 2774 Long Long Message
题链: http://poj.org/problem?id=2774题解: 后缀自动机 使用后缀自动机匹配,思路如下: 即如果当前的x字符匹配失败了,就可以从当前已经匹配的串的后缀去继续匹配. 然后不 ...
- SPOJ - LCS 后缀自动机入门
LCS - Longest Common Substring A string is finite sequence of characters over a non-empty finite set ...
- Longest Common Substring II SPOJ - LCS2 (后缀自动机)
Longest Common Substring II \[ Time Limit: 236ms\quad Memory Limit: 1572864 kB \] 题意 给出\(n\)个子串,要求这\ ...
随机推荐
- ZCMU 1894: Power Eggs
http://acm.zcmu.edu.cn/JudgeOnline/problem.php?id=1894 题意: 有M个鹰蛋,N层楼,鹰蛋的硬度是E,也就是说在1~E层楼扔下去不会碎,E+1层楼扔 ...
- 【LibreOJ】#6354. 「CodePlus 2018 4 月赛」最短路 异或优化建图+Dijkstra
[题目]#6354. 「CodePlus 2018 4 月赛」最短路 [题意]给定n个点,m条带权有向边,任意两个点i和j还可以花费(i xor j)*C到达(C是给定的常数),求A到B的最短距离.\ ...
- [R语言]关联规则1---不考虑items之间的时序关系
本文介绍的是关联规则,分为两部分:第一部分是---不考虑用户购买的items之间严格的时序关系,每个用户有一个“购物篮”,查找其中的关联规则.第二部分--- 考虑items之间的严格的时序关系来分析用 ...
- mongoDB - 日常操作四
python 使用 mongodb easy_install pymongo # 安装(python2.+) import pymongo connection=pymongo.Connection( ...
- <td>内容超出自动换行
td 内容自动换行 table表格td设置宽度后文字太多自动换行 设置table 的 style="table-layout:fixed;" 然后设置td的 style=" ...
- 第6月第4天 AVMutableComposition AVMutableVideoComposition
1. AVMutableComposition is a mutable subclass of AVComposition you use when you want to create a new ...
- lemon spj无效编译器解决方法
反正我是被坑了很久,心里增的敲难过呀! 我曾经无数次的想把它解决掉: 啊啊啊啊啊啊! 什么嘛!什么嘛! 这个空白的框框里到底要填什么嘛!!! 你已经是一个成熟的lemon了,就不能自动识别给个选项吗! ...
- 克隆虚拟机重启之后eth0不见的解决方案
今天用虚拟机克隆多一个虚拟机的时候,发现克隆之后的新虚拟机的网卡eth0在配置之后完全是用不了的,下面说一下我的解决办法,亲测可用. 1.用ipconfig命令查看ip信息的时候会发现虚拟机没有找到e ...
- Javascript - Vue - 指令
指令 v-cloak 解决闪烁,闪烁是指在网速较慢的情况下可能会出现插值表达式{{}}还没有填充数据时会把该表达式直接显示在页面上,如果不希望看到插值表达式则可以使用v-cloak指令,具体做法如下 ...
- PHP+mysql系统报错:PHP message: PHP Warning: Unknown: Failed to write session data (files)
PHP+mysql系统报错:PHP message: PHP Warning: Unknown: Failed to write session data (files) 故障现象,后台页面点击没有 ...
