aced六类股票问题

一.状态转移框架

　　在我们刷题的过程中，很多同学肯定会遇到股票问题这类题目，股票问题有很多种类型，大多数同学都知道要用动态规划去做，但是往往写不对状态转移方程，我刚接触这类问题时也是一头雾水，但是掌握了问题的关键点之后，这类问题就可以迎刃而解了，在此我分享一个方法可以解决所有的股票问题。

　　股票问题一般有以下几种限制条件：交易次数，有无冷冻期（指完成一次交易之后的冷冻期），每次交易有无手续费。所以我们的dp数组有三个状态dp[i][k][s]（i表示天数，k表示允许交易的最大次数，s表示当前的状态，0表示没有持股，1表示持股）。比如说dp[3][2][1]表示今天是第三天，我现在手上持有股票，至今最多进行两次交易。有了dp数组的定义，我们开始研究状态的转移情况，可以画个状态转移图。

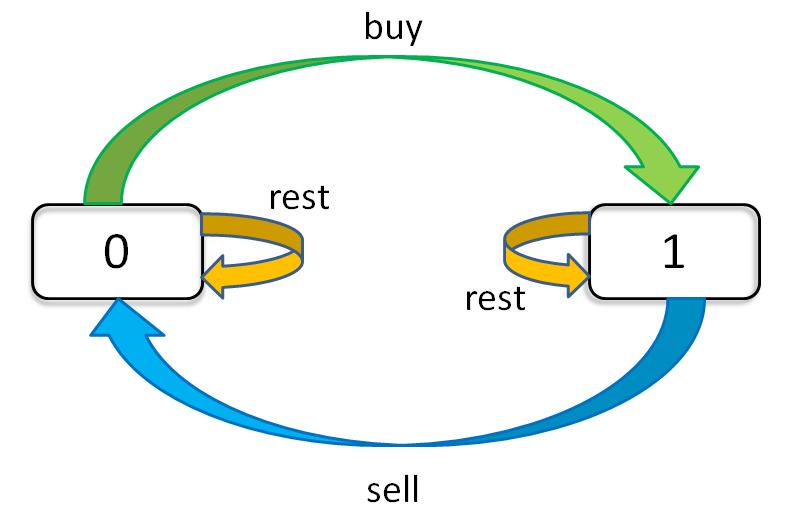
通过此图可以清楚地看到每种状态（0和1）都是如何转移而来的，根据此图我们写一下状态转移方程。

dp[i][k][0]=max(dp[i-1][k][0],dp[i-1][k][1]+prices[i])。今天我没有持有股票有两种可能：1.昨天本来就没有持股，今天选择休息，所以今天还是没有持股2.昨天持有股票，今天sell了，所以我今天没有持股了。

dp[i][k][1]=max(dp[i-1][k][1],dp[i-1][k-1][0]-prices[i])。 今天我持股有两种可能：1.昨天就持股，今天休息，所以今天还持股。2.昨天没有持股，今天buy了，所以今天持股了。

在此我们选择了在buy的时候把k减小了1，当然你也可以在sell的时候减1，一样的。

至此为此，我们完成了动态规划的前两个步骤，最后一个步骤是定义初始值。

dp[-1][k][0] = 0
解释：因为 i 是从 0 开始的，所以 i = -1 意味着还没有开始，这时候的利润当然是 0 。
dp[-1][k][1] = -infinity
解释：还没开始的时候，是不可能持有股票的，用负无穷表示这种不可能。
dp[i][0][0] = 0
解释：因为 k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0 。
dp[i][0][1] = -infinity
解释：不允许交易的情况下，是不可能持有股票的，用负无穷表示这种不可能。

把上面的状态转移方程总结一下：

初始值：
dp[-1][k][0] = dp[i][0][0] = 0
dp[-1][k][1] = dp[i][0][1] = -infinity

状态转移方程：
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

二.aced题目

　　1.第一题（k=1）

直接套状态转移方程，根据 base case，可以做一些化简：

dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], dp[i-1][0][0] - prices[i])
= max(dp[i-1][1][1], -prices[i])
解释：k = 0 的 base case，所以 dp[i-1][0][0] = 0。

现在发现 k 都是 1，不会改变，即 k 对状态转移已经没有影响了。
可以进行进一步化简去掉所有 k：
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], -prices[i])

　　2.第二题（k=+infinity）

如果 k 为正无穷，那么就可以认为 k 和 k - 1 是一样的。可以这样改写框架：

dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
= max(dp[i-1][k][1], dp[i-1][k][0] - prices[i])

我们发现数组中的 k 已经不会改变了，也就是说不需要记录 k 这个状态了：
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])

　　3.第三题（k = +infinity with cooldown）

每次 sell 之后要等一天才能继续交易。只要把这个特点融入上一题的状态转移方程即可：

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
解释：第 i 天选择 buy 的时候，要从 i-2 的状态转移，而不是 i-1 。

　　4.第四题（k = +infinity with fee）

每次交易要支付手续费，只要把手续费从利润中减去即可。改写方程：

dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i] - fee)
解释：相当于买入股票的价格升高了。
在第一个式子里减也是一样的，相当于卖出股票的价格减小了。

　　5.第五题（k=2）

k = 2 和前面题目的情况稍微不同，因为上面的情况都和 k 的关系不太大。要么 k 是正无穷，状态转移和 k 没关系了；要么 k = 1，跟 k = 0 这个 base case 挨得近，最后也没有存在感。

这道题 k = 2 和后面要讲的 k 是任意正整数的情况中，对 k 的处理就凸显出来了。我们直接写代码，边写边分析原因。

原始的动态转移方程，没有可化简的地方
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
按照之前的代码，我们可能想当然这样写代码（错误的）：

int k = 2;
int[][][] dp = new int[n][k + 1][2];
for (int i = 0; i < n; i++)
if (i - 1 == -1) { /* 处理一下 base case*/ }
dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
}
return dp[n - 1][k][0];
为什么错误？我这不是照着状态转移方程写的吗？

还记得前面总结的「穷举框架」吗？就是说我们必须穷举所有状态。其实我们之前的解法，都在穷举所有状态，只是之前的题目中 k 都被化简掉了。这道题由于没有消掉 k 的影响，所以必须要对 k 进行穷举：

int max_k = 2;
int[][][] dp = new int[n][max_k + 1][2];
for (int i = 0; i < n; i++) {
for (int k = max_k; k >= 1; k--) {
if (i - 1 == -1) { /*处理 base case */ }
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
}
}
// 穷举了 n × max_k × 2 个状态，正确。
return dp[n - 1][max_k][0];

　　6.第六题（k = any integer）

有了上一题 k = 2 的铺垫，这题应该和上一题的第一个解法没啥区别。但是出现了一个超内存的错误，原来是传入的 k 值会非常大，dp 数组太大了。现在想想，交易次数 k 最多有多大呢？

一次交易由买入和卖出构成，至少需要两天。所以说有效的限制 k 应该不超过 n/2，如果超过，就没有约束作用了，相当于 k = +infinity。这种情况是之前解决过的。

直接把之前的代码重用：

int maxProfit_k_any(int max_k, int[] prices) {
int n = prices.length;
if (max_k > n / 2)
return maxProfit_k_inf(prices);

int[][][] dp = new int[n][max_k + 1][2];
for (int i = 0; i < n; i++)
for (int k = max_k; k >= 1; k--) {
if (i - 1 == -1) { /* 处理 base case */ }
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
}
return dp[n - 1][max_k][0];
}

三.总结　

　　本文给大家讲了如何通过状态转移的方法解决复杂的问题，用一个状态转移方程秒杀了 6 道股票买卖问题，现在想想，其实也不算难对吧？这已经属于动态规划问题中较困难的了。

关键就在于列举出所有可能的「状态」，然后想想怎么穷举更新这些「状态」。一般用一个多维 dp 数组储存这些状态，从 base case 开始向后推进，推进到最后的状态，就是我们想要的答案。想想这个过程，你是不是有点理解「动态规划」这个名词的意义了呢？

最后我们列出六道股票问题的题目链接，供大家去练习。

https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/

https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii

https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iii

https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iv

https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown

https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee