SQL基础教程（第2版）第7章 集合运算：7-1 表的加减法

第7章 集合运算：7-1 表的加减法

---

● 集合运算就是对满足同一规则的记录进行的加减等四则运算。
● 使用UNION（并集）、 INTERSECT（交集）、 EXCEPT（差集）等集合运算符来进行集合运算。
● 集合运算符可以去除重复行。
● 如果希望集合运算符保留重复行，就需要使用ALL选项。

---

■什么是集合运算

集合在数学领域表示“（各种各样的）事物的总和”，在数据库领域表示记录的集合。具体来说，表、视图和查询的执行结果都是记录的集合。

■表的加法——UNION
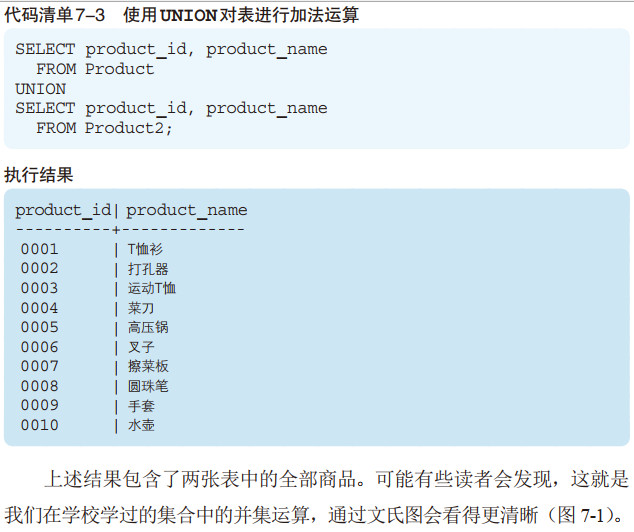
首先为大家介绍的集合运算符是进行记录加法运算的 UNION（并集）。

代码清单7-1　创建表Product2（商品2）

CREATE TABLE Product2
(product_id      CHAR(4)      NOT NULL,
 product_name    VARCHAR(100) NOT NULL,
 product_type    VARCHAR(32)  NOT NULL,
 sale_price      INTEGER      ,
 purchase_price  INTEGER      ,
 regist_date      DATE         ,
 PRIMARY KEY (product_id));

List7_1.sql

商品编号（product_id）为“0001”~“0003”的商品与之前Product表中的商品相同;

而编号为“0009”的“手套”和“0010”的“水壶”是 Product 表中没有的商品。

--MySQL
START TRANSACTION;

INSERT INTO Product2 VALUES ('', 'T恤', '衣服', 1000, 500, '2009-09-20');
INSERT INTO Product2 VALUES ('', '打孔器', '办公用品', 500, 320, '2009-09-11');
INSERT INTO Product2 VALUES ('', '运动T恤', '衣服', 4000, 2800, NULL);
INSERT INTO Product2 VALUES ('', '手套', '衣服', 800, 500, NULL);
INSERT INTO Product2 VALUES ('', '水壶', '厨房用具', 2000, 1700, '2009-09-20');

COMMIT;

--MySQL

■集合运算的注意事项

■注意事项① ——作为运算对象的记录的列数必须相同

■注意事项③——可以使用任何SELECT语句，但ORDER BY子句只能在最后使用一次
通过 UNION 进行并集运算时可以使用任何形式的 SELECT 语句，之前学过的 WHERE、 GROUP BY、 HAVING 等子句都可以使用。
但是ORDER BY 只能在最后使用一次（代码清单 7-4）。

SELECT product_id, product_name
  FROM Product
 WHERE product_type = '厨房用具'
UNION
SELECT product_id, product_name
  FROM Product2
 WHERE product_type = '厨房用具'
ORDER BY product_id;

■包含重复行的集合运算——ALL选项

■选取表中公共部分——INTERSECT

■记录的减法——EXCEPT

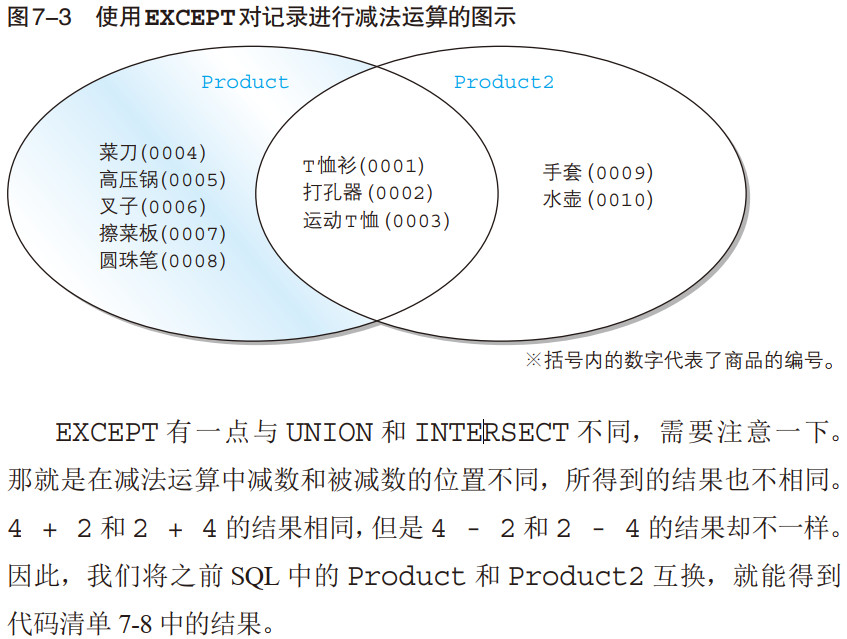
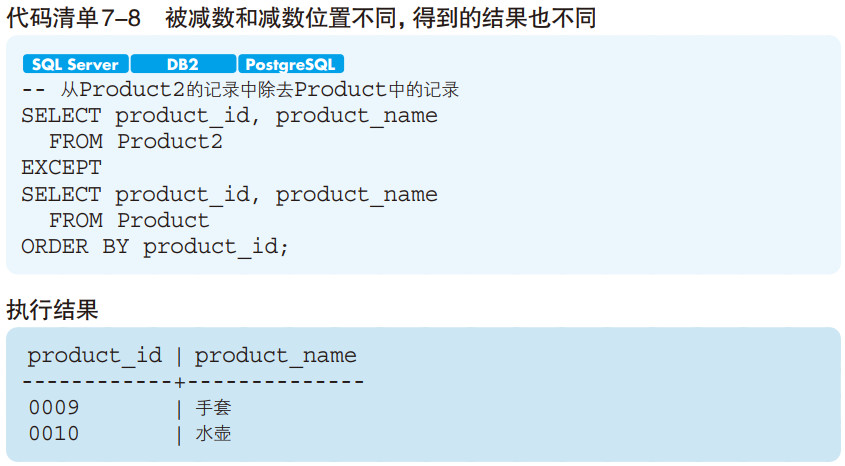
最后要给大家介绍的集合运算符就是进行减法运算的 EXCEPT（差集），其语法也与 UNION 相同（代码清单 7-7）。