HDU 1421 搬寝室 解题报告（超详细）

**搬寝室

Time Limit: 2000/1000 MS Memory Limit: 65536/32768 K

Problem Description

搬寝室是很累的,xhd深有体会.时间追述2006年7月9号,那天xhd迫于无奈要从27号楼搬到3号楼,因为10号要封楼了.看着寝室里的n件物品,xhd开始发呆,因为n是一个小于2000的整数,实在是太多了,于是xhd决定随便搬2k件过去就行了.但还是会很累,因为2k也不小是一个不大于n的整数.幸运的是xhd根据多年的搬东西的经验发现每搬一次的疲劳度是和左右手的物品的重量差的平方成正比(这里补充一句,xhd每次搬两件东西,左手一件右手一件).例如xhd左手拿重量为3的物品,右手拿重量为6的物品,则他搬完这次的疲劳度为(6-3)^2 = 9.现在可怜的xhd希望知道搬完这2*k件物品后的最佳状态是怎样的(也就是最低的疲劳度),请告诉他吧.

Input

每组输入数据有两行,第一行有两个数n,k(2<=2*k<=n<2000).第二行有n个整数分别表示n件物品的重量(重量是一个小于2^15的正整数).

Output

对应每组输入数据,输出数据只有一个表示他的最少的疲劳度,每个一行.

Sample Input

2 1 1 3

Sample Output

4

Author

xhd

解题思路：

题目意思为求n个物品，拿k对使得消耗的体力最少，或者说是这k对物品，每一对中两件物品的质量差平方最小，所以要使得质量差的平方小，只能排序后取质量相邻两个物品作为一对；

现在设dp[i][j]为前i件物品组成k对所消耗的体力最小；

这时分两种情况含有第i件物品和不含有第i件物品（即第i件物品是不是含在第j对里）

1.含有i件物品 则有 dp[i][j]=dp[i-2][j-1]+(ob[i-1]-ob[i])(ob[i-1]-ob[i])

2.不含第i件物品则有 dp[i][j]=dp[i-1][j]

所以动态转移方程为 ：dp[i][j]=min(dp[i-2][j-1]+(ob[i-1]-ob[i])(ob[i-1]-ob[i]),dp[i-1][j]);

我们用一组数据来解释状态转移方程。



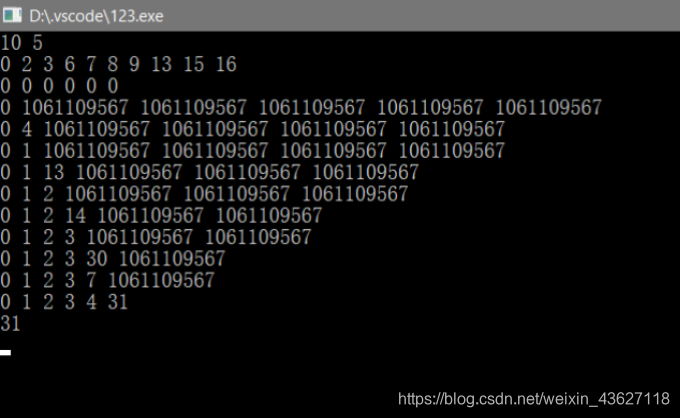
以最大值0x3f3f3f3f为分界线，为什么要使用0x3f3f3f3f作为最大值，全是个人习惯，在这里用0x7f7f7f7f也可以。但是在有些题目中当两个无穷大相加的时候进位变为负号，成为极小值，为了避免这种情况出现，用0x3f3f3f3f作为最大值，比无穷大的一半稍小，但是也是一个极大的数，用来做无穷大最好不过。

注 ：

int型是4个字节 一个字节8个位 0x7f7f7f7f 是十六进制 也就是4个0x7f ,一个0x7f 转化为二进制就是 01111111

因为是int型 第一个位是符号位 ，因而在int 型中 0x7f7f7f7f也就是无穷大的意思。

以无穷大为界限第一阶梯代表只要当前值可选就选消耗的体力。

第二阶梯代表有一个数据没有选择的最优消耗体力，他的选择机制是选当前两个，或者跳过去一个，如果跳过这一个比都选要轻松，他会选择跳过当前值，于是这就是状态转移方程，选择机制是选当前值，或者不选当前值。

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
long long int ob[2001];
long long int dp[2001][2001];
const long long int max1=0x3f3f3f3f;
int main()
{
    int n,k;
    while(cin>>n>>k)
    {
      //  memset(dp,max1,sizeof(dp));  memset 最好用来赋值0或-1，不然会出错。
        memset(ob,0,sizeof(ob));
        for(int i=1;i<=n;i++)
            cin>>ob[i];
        sort(ob+1,ob+n+1);
        ob[0]=0;
        for(int i=0;i<=n;i++)
        {
            for(int j=0;j<=n;j++)
            {
                dp[i][j]=max1;

            }
        }
        for(int i=0;i<=n;i++) dp[i][0]=0;
        for(int i=2;i<=n+1;i++)
        {
            for(int j=1;j<=k;j++)
                dp[i][j]=min(dp[i-2][j-1]+(ob[i-1]-ob[i])*(ob[i-1]-ob[i]),dp[i-1][j]);
        }
       /* for(int i=0;i<n+1;i++)   遇到不会的题目，就按照他的状态转移方程操作后输出dp数组，来研究状态转移方程的实现过程。
        {

            for(int j=0;j<n+1;j++)
            {
                cout<<dp[i][j]<<' ';
            }
            cout<<endl;
        }*/
        cout<<dp[n][k]<<endl;
    }
}