python实现PCA算法原理
PCA主成分分析法的数据主成分分析过程及python原理实现
1、对于主成分分析法,在求得第一主成分之后,如果需要求取下一个主成分,则需要将原来数据把第一主成分去掉以后再求取新的数据X’的第一主成分,即为原来数据X的第二主成分,循环往复即可。
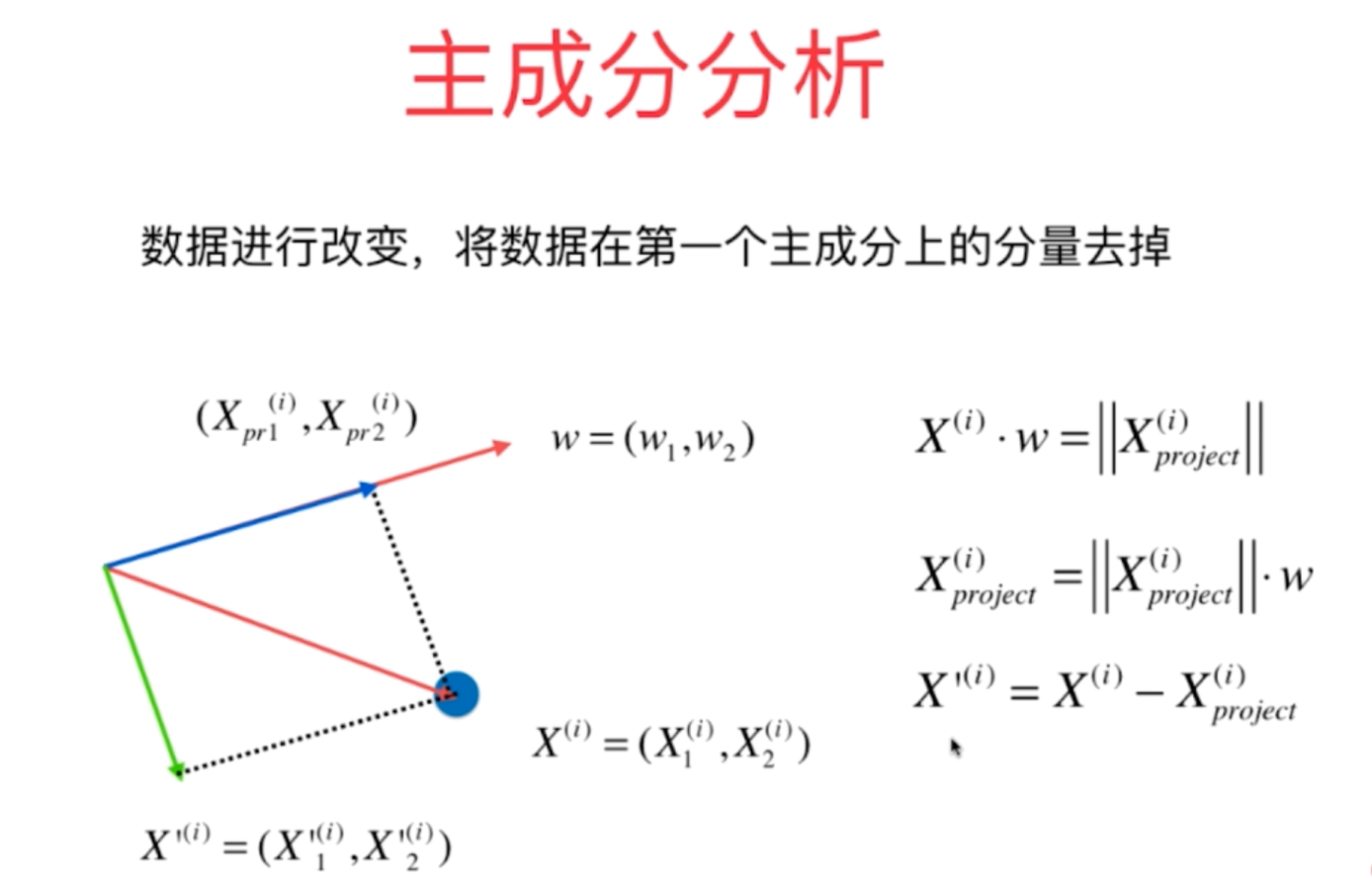
2、利用PCA算法的原理进行数据的降维,其计算过程的数学原理如下所示,其降维的过程会丢失一定的信息,因此采用恢复过程恢复原来的高维数据后,它会恢复为原来数据在新的主成分上的映射点,而不再是原来的坐标点。
(1)高维数据的降维(从n维降到k维数据)

(2)从降维得到k维数据恢复到原来的n维数据集
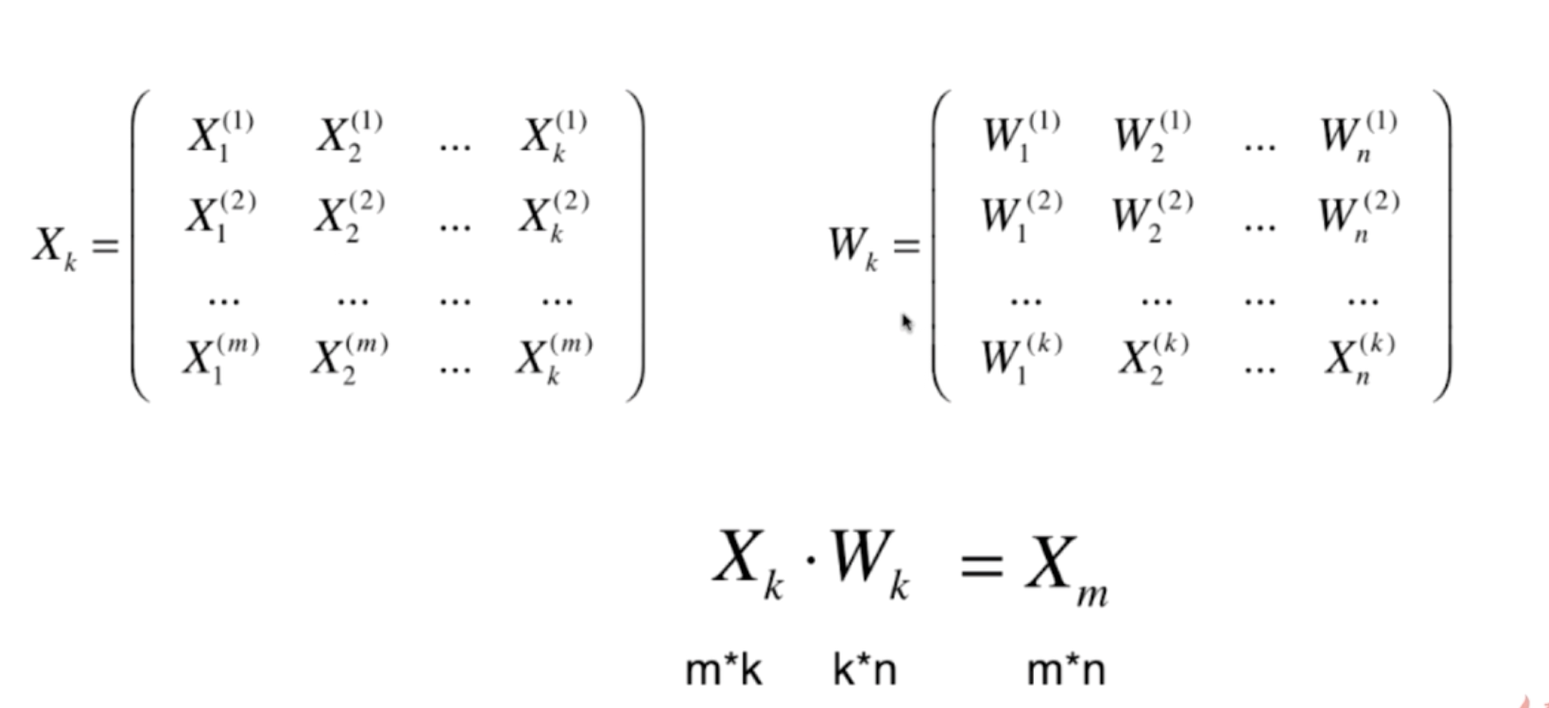
3、具体的数据降维实现原理代码如下所示:
import numpy as np
import matplotlib.pyplot as plt
x=np.empty((100,2))
x[:,0]=np.random.uniform(0.0,100.0,size=100)
x[:,1]=0.75*x[:,0]+3.0*np.random.normal(0,3,size=100)
plt.figure()
plt.scatter(x[:,0],x[:,1])
plt.show() #demean操作函数定义
def demean(x):
return x-np.mean(x,axis=0)
print(x)
print(np.mean(x,axis=0))
print(demean(x))
print(np.mean(demean(x),axis=0))
x_demean=demean(x) #梯度上升法的函数定义
def f(w,x):
return np.sum((x.dot(w))**2)/len(x)
def df_math(w,x):
return x.T.dot(x.dot(w))*2/len(x)
def df_debug(w,x,epsilon=0.00001):
res=np.empty(len(x))
for i in range(len(x)):
w1=w.copy()
w1[i]=w1[i]+epsilon
w2= w.copy()
w2[i] =w2[i]-epsilon
res[i]=(f(w1,x)-f(w2,x))/(2*epsilon)
return res
def derection(w):
return w/np.linalg.norm(w)
def gradient_ascent1(x,eta,w_initial,erro=1e-8, n=1e6):
w=w_initial
w=derection(w)
i=0
while i<n:
gradient =df_math(w,x)
last_w = w
w = w + gradient * eta
w = derection(w) #注意1:每次都需要将w规定为单位向量
if (abs(f(w,x) - f(last_w,x))) < erro:
break
i+=1
return w
w0=np.random.random(x.shape[1]) #注意2:不能从0向量开始
print(w0)
eta=0.001 #注意3:不能将数据进行标准化,即不可以使用standardscaler进行数据标准化
w1=gradient_ascent1(x_demean,eta,w0)
print(w1)
q=np.linspace(-40,40)
Q=q*w1[1]/w1[0]
plt.figure(1)
plt.scatter(x[:,0],x[:,1])
plt.plot(q,Q,"r")
print(w1[1]/w1[0]) #求取数据的前n个的主成分,循环往复即可
x2=np.empty(x.shape)
for i in range(len(x)):
x2[i]=x_demean[i]-x_demean[i].dot(w1)*w1
plt.figure()
plt.scatter(x2[:,0],x2[:,1],color="g")
plt.show()
w00=np.random.random(x.shape[1])
print(w00)
w2=gradient_ascent1(x2,eta,w00)
print(w2) #求取n维数据的前n个主成分的封装函数
def first_n_compnent(n,x,eta=0.001,erro=1e-8, m=1e6):
x_pca=x.copy()
x_pca=demean(x_pca)
res=[]
for i in range(n):
w0=np.random.random(x.shape[1])
w=gradient_ascent1(x_pca,eta,w0)
res.append(w)
x_pca=x_pca-x_pca.dot(w).reshape(-1,1)*w
return res
print(first_n_compnent(2,x))
实际的运行效果如下所示:
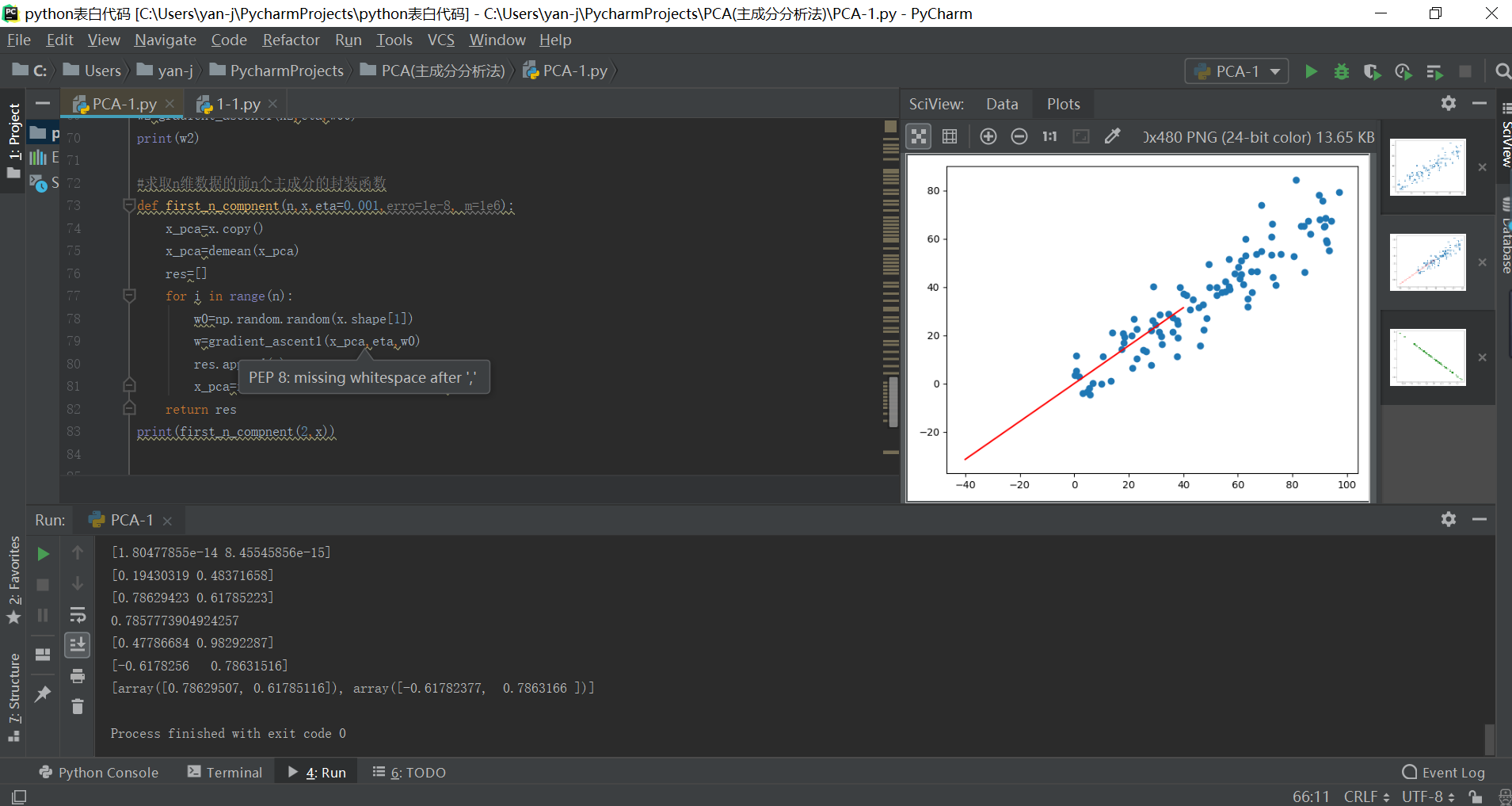
python实现PCA算法原理的更多相关文章
- 主成分分析 PCA算法原理
对同一个体进行多项观察时,必定涉及多个随机变量X1,X2,…,Xp,它们都是的相关性, 一时难以综合.这时就需要借助主成分分析 (principal component analysis)来概括诸多信 ...
- 深入学习主成分分析(PCA)算法原理(Python实现)
一:引入问题 首先看一个表格,下表是某些学生的语文,数学,物理,化学成绩统计: 首先,假设这些科目成绩不相关,也就是说某一科目考多少分与其他科目没有关系,那么如何判断三个学生的优秀程度呢?首先我们一眼 ...
- 三种方法实现PCA算法(Python)
主成分分析,即Principal Component Analysis(PCA),是多元统计中的重要内容,也广泛应用于机器学习和其它领域.它的主要作用是对高维数据进行降维.PCA把原先的n个特征用数目 ...
- 梯度迭代树(GBDT)算法原理及Spark MLlib调用实例(Scala/Java/python)
梯度迭代树(GBDT)算法原理及Spark MLlib调用实例(Scala/Java/python) http://blog.csdn.net/liulingyuan6/article/details ...
- 手指静脉细化算法过程原理解析 以及python实现细化算法
原文作者:aircraft 原文地址:https://www.cnblogs.com/DOMLX/p/8672489.html 文中的一些图片以及思想很多都是参考https://www.cnblogs ...
- Python使用三种方法实现PCA算法[转]
主成分分析(PCA) vs 多元判别式分析(MDA) PCA和MDA都是线性变换的方法,二者关系密切.在PCA中,我们寻找数据集中最大化方差的成分,在MDA中,我们对类间最大散布的方向更感兴趣. 一句 ...
- Python的主成分分析PCA算法
这篇文章很不错:https://blog.csdn.net/u013082989/article/details/53792010 为什么数据处理之前要进行归一化???(这个一直不明白) 这个也很不错 ...
- 机器学习--主成分分析(PCA)算法的原理及优缺点
一.PCA算法的原理 PCA(principle component analysis),即主成分分析法,是一个非监督的机器学习算法,是一种用于探索高维数据结构的技术,主要用于对数据的降维,通过降维可 ...
- Python实现的选择排序算法原理与用法实例分析
Python实现的选择排序算法原理与用法实例分析 这篇文章主要介绍了Python实现的选择排序算法,简单描述了选择排序的原理,并结合实例形式分析了Python实现与应用选择排序的具体操作技巧,需要的朋 ...
随机推荐
- linux 环境下安装 MySQL
参考: Linux安装MySQL5.7 注意: 安装后 出现 navicat MySQL连接Linux下MySQL的及2003错误 需要看下 虚拟机的防火墙是否关闭!!!
- 确定BP神经网络中的节点数
输入层 输入层节点数=输入向量维数 MNIST例子中,单张MNIST图片大小为28*28,reshape为一维数组,长度为784,所以输入层节点数为784: network = Network([78 ...
- 牛客跨年AK场-小sum的假期安排
链接:https://ac.nowcoder.com/acm/contest/3800/G来源:牛客网 题目描述 小 sun 非常喜欢放假,尤其是那种连在一起的长假,在放假的时候小 sun 会感到快乐 ...
- 通过LAMP部署phpMyAdmin、wordpress(https)、discuz
1.安装启动LAMP 安装环境: CentOS Linux release 7.5.1804 安装包: # yum -y install httpd php php-mysql mariadb-ser ...
- 树莓派4B踩坑指南 - (6)安装常用软件及相关设置
安装软件 安装LibreOffice中文包 sudo apt-get install libreoffice-l10n-zh-cn sudo reboot 安装codeblocks并汉化: sudo ...
- spring aop @after和@before之类的注解,怎么指定多个切点
有如下两个切点: @Pointcut("execution(public * com.wyh.data.controller.DepartmentController.*(..))" ...
- 操作系统OS - 常见系统的调度算法
https://en.wikipedia.org/wiki/Scheduling_(computing) 在wiki的下面可以找到
- Python实现一个LRU
class Node: key = None value = None pre = None next = None def __init__(self, key, value): self.key ...
- Django中的prefetch_related()函数优化
对于多对多字段(ManyToManyField)和一对多字段, 可以使用prefetch_related()来进行优化 prefetch_related()和select_related()的设计目的 ...
- JAVA中final关键字的作用
一.final关键字的功能概述 final关键字可以用来修饰引用.方法和类. 1.用来修饰一个引用 如果引用为基本数据类型,则该引用为常量,该值无法修改: 如果引用为引用数据类型,比如对象.数组,则该 ...
