Python实现二叉树的前序、中序、后序、层次遍历

  有关树的理论部分描述：《数据结构与算法》-4-树与二叉树；

  下面代码均基于python实现，包含：

• 二叉树的前序、中序、后序遍历的递归算法和非递归算法；
• 层次遍历；
• 由前序序列、中序序列重构二叉树；
• 由后序序列、中序序列重构二叉树；

# -*- coding: utf-8 -*-
# @Time: 2019-04-15 18:35
# @Author: chen

class NodeTree:
    def __init__(self, root=None, lchild=None, rchild=None):
        """创建二叉树
        Argument:
            lchild: BinTree
                左子树
            rchild: BinTree
                右子树

        Return:
            Tree
        """
        self.root = root
        self.lchild = lchild
        self.rchild = rchild

class BinTree:

    # -----------前序遍历 ------------
    # 递归算法
    def pre_order_recursive(self, T):
        if T == None:
            return
        print(T.root, end=' ')
        self.pre_order_recursive(T.lchild)
        self.pre_order_recursive(T.rchild)

    # 非递归算法
    def pre_order_non_recursive(self, T):
        """借助栈实现前驱遍历
        """
        if T == None:
            return
        stack = []
        while T or len(stack) > 0:
            if T:
                stack.append(T)
                print(T.root, end=' ')
                T = T.lchild
            else:
                T = stack[-1]
                stack.pop()
                T = T.rchild

    # -----------中序遍历 ------------
    # 递归算法
    def mid_order_recursive(self, T):
        if T == None:
            return
        self.mid_order_recursive(T.lchild)
        print(T.root, end=' ')
        self.mid_order_recursive(T.rchild)

    # 非递归算法
    def mid_order_non_recursive(self, T):
        """借助栈实现中序遍历
        """
        if T == None:
            return
        stack = []
        while T or len(stack) > 0:
            if T:
                stack.append(T)
                T = T.lchild
            else:
                T = stack.pop()
                print(T.root, end=' ')
                T = T.rchild

    # -----------后序遍历 ------------
    # 递归算法
    def post_order_recursive(self, T):
        if T == None:
            return
        self.post_order_recursive(T.lchild)
        self.post_order_recursive(T.rchild)
        print(T.root, end=' ')

    # 非递归算法
    def post_order_non_recursive(self, T):
        """借助两个栈实现后序遍历
        """
        if T == None:
            return
        stack1 = []
        stack2 = []
        stack1.append(T)
        while stack1:
            node = stack1.pop()
            if node.lchild:
                stack1.append(node.lchild)
            if node.rchild:
                stack1.append(node.rchild)
            stack2.append(node)
        while stack2:
            print(stack2.pop().root, end=' ')
        return

    # -----------层次遍历 ------------
    def level_order(self, T):
        """借助队列（其实还是一个栈）实现层次遍历
        """
        if T == None:
            return
        stack = []
        stack.append(T)
        while stack:
            node = stack.pop(0)  # 实现先进先出
            print(node.root, end=' ')
            if node.lchild:
                stack.append(node.lchild)
            if node.rchild:
                stack.append(node.rchild)

    # ----------- 前序遍历序列、中序遍历序列 —> 重构二叉树 ------------
    def tree_by_pre_mid(self, pre, mid):
        if len(pre) != len(mid) or len(pre) == 0 or len(mid) == 0:
            return
        T = NodeTree(pre[0])
        index = mid.index(pre[0])
        T.lchild = self.tree_by_pre_mid(pre[1:index+1], mid[:index])
        T.rchild = self.tree_by_pre_mid(pre[index+1:], mid[index+1:])
        return T

    # ----------- 后序遍历序列、中序遍历序列 —> 重构二叉树 ------------
    def tree_by_post_mid(self, post, mid):
        if len(post) != len(mid) or len(post) == 0 or len(mid) == 0:
            return
        T = NodeTree(post[-1])
        index = mid.index(post[-1])
        T.lchild = self.tree_by_post_mid(post[:index], mid[:index])
        T.rchild = self.tree_by_post_mid(post[index:-1], mid[index+1:])
        return T

if __name__ == '__main__':

    # ----------- 测试：前序、中序、后序、层次遍历 -----------
    # 创建二叉树
    nodeTree = NodeTree(1,
             lchild=NodeTree(2,
                         lchild=NodeTree(4,
                                     rchild=NodeTree(7))),
             rchild=NodeTree(3,
                         lchild=NodeTree(5),
                         rchild=NodeTree(6)))
    T = BinTree()
    T.pre_order_recursive(nodeTree)  # 前序遍历-递归
    print('\n')
    T.pre_order_non_recursive(nodeTree)  # 前序遍历-非递归
    print('\n')
    T.mid_order_recursive(nodeTree)  # 中序遍历-递归
    print('\n')
    T.mid_order_non_recursive(nodeTree)  # 前序遍历-非递归
    print('\n')
    T.post_order_recursive(nodeTree)  # 后序遍历-递归
    print('\n')
    T.post_order_non_recursive(nodeTree)  # 前序遍历-非递归
    print('\n')
    T.level_order(nodeTree)  # 层次遍历
    print('\n')

    print('==========================================================================')

    # ----------- 测试：由遍历序列构造二叉树 -----------
    T = BinTree()
    pre = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']
    mid = ['B', 'C', 'A', 'E', 'D', 'G', 'H', 'F', 'I']
    post = ['C', 'B', 'E', 'H', 'G', 'I', 'F', 'D', 'A']

    newT_pre_mid = T.tree_by_pre_mid(pre, mid)  # 由前序序列、中序序列构造二叉树
    T.post_order_recursive(newT_pre_mid)  # 获取后序序列
    print('\n')

    newT_post_mid = T.tree_by_post_mid(post, mid)  # 由后序序列、中序序列构造二叉树
    T.pre_order_recursive(newT_post_mid)  # 获取前序序列

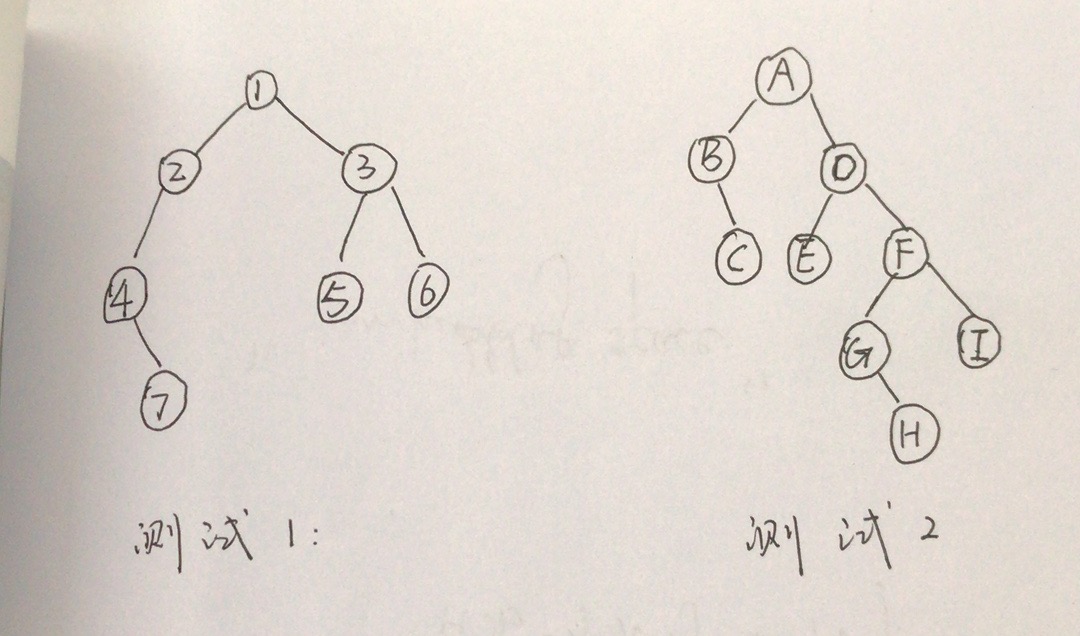
  测试用的两个二叉树：