LeetCode935

问题：935. 骑士拨号器

国际象棋中的骑士可以按下图所示进行移动：

 .           

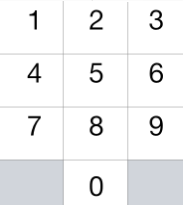
这一次，我们将 “骑士” 放在电话拨号盘的任意数字键（如上图所示）上，接下来，骑士将会跳 N-1 步。每一步必须是从一个数字键跳到另一个数字键。

每当它落在一个键上（包括骑士的初始位置），都会拨出键所对应的数字，总共按下 N 位数字。

你能用这种方式拨出多少个不同的号码？

因为答案可能很大，所以输出答案模 10^9 + 7。

示例 1：

输入：1
输出：10

示例 2：

输入：2
输出：20

示例 3：

输入：3
输出：46

提示：

• 1 <= N <= 5000

链接：https://leetcode-cn.com/contest/weekly-contest-109/problems/knight-dialer/

分析：

如果只拨号1次，10个数字都有可能，结果返回10，

如果1次以上，不可能有5，而且其他9个数字相互之间可达

建立直接的goto表，

gototables[0] = vector < int > {4, 6};
gototables[1] = vector < int > {8, 6};
gototables[2] = vector < int > {7, 9};
gototables[3] = vector < int > {4, 8};
gototables[4] = vector < int > {3, 9, 0};
gototables[5] = vector < int > {};
gototables[6] = vector < int > {1, 7, 0};
gototables[7] = vector < int > {2, 6};
gototables[8] = vector < int > {1, 3};
gototables[9] = vector < int > {2, 4};

第一个gototables[0] = vector < int > {4, 6};表示从0可以直接到达4 6，反之，可以从4 6 到达0.

拨第K次的号码数取决于前一次0-9（5除外，或者5一直都是0）的个数。

比如拨3次的号码数，取决于拨第二次后的0-9个数，

用公式表示的话，

goto[i]=T[m,n...]

i表示一个数组，T是一个数字，里面的m、n，和i可以互相到达

Num(i,j)表示拨号j次后i的个数

则Num(i,j)=ΣT(T(i),j-1)

前面几次结果如下表：

	可达列表			数字	1（次数）	2	3	4
		6	4	0	1	2	6（0对应4 6，前一次值均为3）	12
		8	6	1	1	2	5（1对应8 6，前一次值2 3）	10
		9	7	2	1	2	4	10
		8	4	3	1	2	5	10
	9	3	0	4	1	3	6	16
				5	1
	7	1	0	6	1	3	6	16
		6	2	7	1	2	5	10
		3	1	8	1	2	4	10
		4	2	9	1	2	5	10
				总和	10	20	46

AC Code：

class Solution935
{
public:

	map<int, vector<int> > gototables = {}; //从一个键可以到达的键的表
	long long Mod = 1000000007;
	int knightDialer(int N)
	{
		init();
		if (N == 1)
		{
			return 10;
		}
		long long ret=0;
		vector<long long> nums; //记录拨号第M次后各个数字的个数
		for (int i = 0; i < 10; i++)
		{
			nums.emplace_back(0);
		}
		for (int i = 1; i < N; i++)
		{
			if (i == 1)
			{
				for (int j = 0; j < nums.size(); j++)  //第一次拨号后的每个数字个数
				{
					nums[j] += this->gototables[j].size();
				}
			}
			else
			{
				vector<long long> pre;  //记录前一次的数字个数，用来更新本次拨号后的未位各个数字个数
				for (int t = 0; t < nums.size(); t++)
				{
					pre.emplace_back(nums[t]);
				}
				for (int j = 0; j < nums.size(); j++)
				{
					vector<int> tmp = this->gototables[j];  //该位数字可以按到的下一个，同时也是可以按到该位数字的前一个数字
					long long local = 0;
					for (int m = 0; m < tmp.size(); m++)
					{
						local += pre[tmp[m]];  //正好用0-9下标存储对应数字的个数，直接累加即可
					}
					local %= this->Mod; //余数定理可以先求余后累加
					nums[j] = local; //得到该位数字的个数
				}
			}
		}
		ret = 0;
		for (int i = 0; i < nums.size(); i++)
		{
			ret += nums[i];  //各个数字为最终尾数的个数和即为结果
		}
		ret %= this->Mod;
		return ret;
	}

	void init()
	{
		gototables[0] = vector < int > {4, 6};
		gototables[1] = vector < int > {8, 6};
		gototables[2] = vector < int > {7, 9};
		gototables[3] = vector < int > {4, 8};
		gototables[4] = vector < int > {3, 9, 0};
		gototables[5] = vector < int > {};
		gototables[6] = vector < int > {1, 7, 0};
		gototables[7] = vector < int > {2, 6};
		gototables[8] = vector < int > {1, 3};
		gototables[9] = vector < int > {2, 4};
	}
};　　

其他：

1.最开始通过递归来做，深度优先模拟拨号过程，结果超时

2.没认真考虑，单纯优化为能够到达下一次的个数，即初始能按下两个键的有七个，能按下3个键的有2个，第二次后能按下两个键的有7*2个，能按下三个键的有2*3个，结果20也是符合，第三次7*2*2=28,2*3*3=18,28+18=46也符合，结果错了......，一来第四次后测试太多不方便验证，二来得出结论太草率，实际上按后尾号为某个数字的个数取悦于前一次能按过来的数字个数和。

3.这个问题折腾了一个多小时，关键在于建立的模型不对，而且手动验证太麻烦，总是出错重来，思维不够清晰。

第一的code：

typedef long long ll;
typedef vector<int> VI;
typedef pair<int,int> PII;

#define REP(i,s,t) for(int i=(s);i<(t);i++)
#define FILL(x,v) memset(x,v,sizeof(x))

const int INF = (int)1E9;
#define MAXN 100005

VI adj[10];
const int mod = 1000000007;
int dp[5005][10];
class Solution {
public:
  int knightDialer(int N) {
    adj[1] = VI({6,8});
    adj[2] = VI({7,9});
    adj[3] = VI({4,8});
    adj[4] = VI({0,3,9});
    adj[6] = VI({0,1,7});
    adj[7] = VI({2,6});
    adj[8] = VI({1,3});
    adj[9] = VI({2,4});
    adj[0] = VI({4,6});
    FILL(dp, 0);
    REP(d,0,10) dp[1][d] = 1;
    REP(i,2,N+1) {
      REP(d,0,10) {
        int pre = dp[i-1][d];
        if (pre == 0) continue;
        REP(k,0,adj[d].size()) {
          int d2 = adj[d][k];
          dp[i][d2] = (dp[i][d2] + pre) % mod;
        }
      }
    }
    int ans = 0;
    REP(d,0,10) ans = (ans + dp[N][d]) % mod;
    return ans;
  }
};

看到code中的dp，想到之前有刻意针对动态规划做过练习，结果用的时候还是没有这个意思，没学好。