HGOI 20191029pm 题解

Promblem A 小学组

给出一个位运算操作符$\oplus \in \{or , and , xor\}$ ，和$n$个$m$维向量$a_i$，其中$a_{i,j} \in \{0,1\}$。

并给出一个最终的目标$m$维向量$x$，求出长度为$k(1\leq k \leq n)$的不重复数组$p_i$的个数，

满足$1 \leq p_i \leq n$，使得$a_{p_1,i}  \oplus a_{p_2 ,i } \oplus ...\oplus a_{p_k,i} = x_i$

对于$100\%$的数据，满足$1 \leq n,m \leq 25$

　　Solution ：

　　　　考虑向量的维度时$m$，且比较小，而且是$0/1$，那么直接可以利用二进制状态压缩的办法将其存储。

　　　　每一次操作对于两个向量的两个相同维度做一次二进制操作，由于二进制的结合律，就相当于直接对整数做这些操作。

　　　　利用二进制运算的交换律可知，在一个确定的$p$的取值集合中交换任意两个数的顺序，不会对答案有任何影响。

　　　　那么这里，一旦一个$p$的集合合法，那么对于所有$p$集合的排列就必然合法。

　　　　注意到，空集不是一个合法的方案。

　　　　利用这两个性质，我们直接就用$O(2^n)$枚举每一个向量取不取就好了，如果合法，就加上对应的排列数。

# pragma GCC optimize()
# include<bits/stdc++.h>
# define ll long long
# define Rint register int
using namespace std;
const int N=;
const int mo=1e9+;
char op;
int n,m,base,t[N],a[N];
ll jc[N],ans;
void dfs(Rint u,Rint cnt,Rint num) {
    if (u == n+) {
        if (cnt == ) return;
        if (num==base)  (ans+=1ll*jc[cnt])%=mo;
        return;
    }
    t[u]=;  dfs(u+,cnt,num);
    t[u]=;
    if (op == '&') dfs(u+,cnt+,(num==)?(a[u]):(num&a[u]));
    else if (op == '|') dfs(u+,cnt+,num|a[u]);
    else if (op == '^') dfs(u+,cnt+,num^a[u]);
}
signed main()
{
  freopen("xx.in","r",stdin);
  freopen("xx.out","w",stdout);
    scanf("%c%d%d",&op,&n,&m);
    jc[]=;for (Rint i=;i<=n;i++) jc[i]=jc[i-]*i%mo;
    for (Rint i=;i<=n;i++) {
        int num=;
        for (Rint j=;j<=m;j++) {
            int u; scanf("%d",&u);
            num=(num<<)+u;
        }
        a[i] = num;
    }
    for (Rint i=;i<=m;i++) {
        int u; scanf("%d",&u);
        base=(base<<)+u;
    }
    dfs(,,);
    printf("%lld\n",ans);
    return ;
}

xx.cpp

 Problem B 普及组

　构造一个合法$n\times n$的矩阵$A$，需要满足下述三个条件：

　 $A_{i,j} \in Z $  ;  对于任意$i$都有$\prod\limits_{j = 1}^{n} A_{i,j} = X$  ;  对于任意$j$都有$\prod\limits_{i = 1}^{n} A_{i,j} = X$

　其中$X$是一个所有询问前就给出的数字，现在有$T$组数据，给出$n$,求出构造矩阵的填法方案数

　所有可能的$X$已知，答案对$998244353$取模。

　对于$100\%$的数据满足$X$的质因子的幂次最多是$2$ , 且$1 \leq n \leq 5\times 10^6 , 1 \leq T \leq 2 \times 10^5$

　Solution :

　　本题有一个$O(T log_2 n)$的奇怪做法。

• 考虑$X = 1$的情况。

　　　　此时相当于将前$n-1$行和$n-1$列都填$-1$或者$1$那么剩余的格子就确定了。答案就是$2^{(n-1)^2}$

• 考虑$X \in Prime$的情况。

　　　　首先将每行每列的乘积都变成$1$，那么就是$2^{(n-1)^2}$种情况，考虑将每行每列的焦点填上一个质数$X$，

　　　　问题就转化为将行和列匹配的方案数，那么考虑一个排列，其下标和值就是一个不同匹配，可以证明，不同的排列，其匹配是不同的。

　　　　所以此时答案就是$n! \times 2^{(n-1)^2} $

• 考虑$X$不含等于$2$次幂次的质因子。

　　　　首先$1$和$-1$的填法并没有什么区别，对于每一个质因子，只是填的位置有区别。

　　　　根据乘法原理，此时答案就是$(n!)^k \times \times 2^{(n-1)^2} $， 其中$k$是不同质因子的个数。

• 考虑$X$只含有$2$次幂次的质因子，即$X = p^2$ ,

　　　　问题就转化填数方式，使得每一行和每一列都恰好填$2$个数。

　　　　这个数列事实上可以通过打表发现规律，$f_i = \left\{\begin{matrix} 1 & i = 0,1\\ f_i = i^2 f_{i-1} - \frac{1}{2} i (i-1)^2 f_{i-2}   & i \geq 2 \end{matrix}\right.$

　　设给出的$X$中有$a$个质因数指数幂次为$1$，$b$个质因数指数幂次为$2$,

　　那么这个询问的答案就是$(n!)^a \times (f_n)^b \times  2^{(n-1)^2} $

　　所以，对于一个询问的时间复杂度就是一个快速幂的复杂度，总时间复杂度为$O(T log_2 n)$

# pragma GCC optimize()
# include <bits/stdc++.h>
# define int long long
# define putchar_ putchar
using namespace std;
const int mo=;
const int Inv2 = ;
const int N=5e6+;
int f[N],jc[N];
int val[N];
vector<int>H;
inline int read()
{
    int X=,w=; char c=;
    while(c<''||c>'') {w|=c=='-';c=getchar();}
    while(c>=''&&c<='') X=(X<<)+(X<<)+(c^),c=getchar();
    return w?-X:X;
}
void write(int x) {
    if (x>) write(x/);
    putchar(x%+'');
}
int Pow(int x,int n) {
    int ans = ;
    while (n) {
        if (n&) ans = ans * x % mo;
        x = x * x % mo;
        n >>= ;
    }
    return ans % mo;
}
int T,x;
void work1()
{
    while (T--) {
        int n=read();
        int ans = Pow(,(n-)*(n-));
        write(ans); putchar_('\n');
    }
    exit();
}
signed main()
{
    f[]=f[]=jc[]=jc[]=;
    for (int i=;i<=;i++)
        f[i]=((i*i%mo*f[i-]%mo-Inv2*i%mo*(i-)%mo*(i-)%mo*f[i-]%mo)%mo+mo)%mo,
        jc[i] = jc[i-] * i % mo;
    x=read(); T=read(); if (x == ) work1();
    int a =  , b = ;
        if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    if(x==)a=,b=;
    while (T--) {
        int n = read();
        int ans1=jc[n]%mo;
        int ans2=f[n]%mo;
        int ans = Pow(ans1,a) * Pow(ans2,b) % mo * Pow(,(n-)*(n-)) % mo;
        write(ans); putchar_('\n');
    }
    return ;
}

pj.cpp

 Problem C 提高组　

　有$T$组询问，给出$x,y$,求出最长下降子序列长度不超过$2$的排列$p$且$p_x = y$。

　输出排列数对$10^9 + 7$取模的答案。

　对于$100\%$的数据满足$1 \leq T \leq 10^6 , 1 \leq n \leq 10^7$

Solution :

　　考虑如果没有$p_x = y$限制怎么做。

　　设$f[i][j]$表示当前考虑到第$i$个位置，当前填的最大数为$j$。

　　如果$i \leq j$那么$i$之前至少存在一个数字未填，此时必须补一个数，且恰好在那个断点的上面一个数的位置。

　　

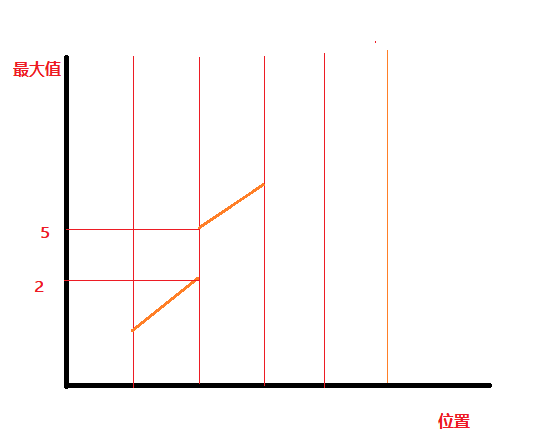
　如上图所示，在当前决策点的时候只会去填补$3$的的空缺，而不会直接填$4$.

　这是因为，如果这个地方填了$4$，那么之后必然会填$3$，这样就会使得最长下降子序列为$3$了。

　于是，我们就可以$DP$来转移，当前决策点为$(i,j)$，转移到

• $f[i+1][k] , (k > j)$（此时将不会管中间空缺部位,选一个更大的数填）
• $f[i][j] (i < j)$ （此时填写最小的空缺的数）

　接下来我们考虑$p_x = y$的限制，不妨设$x < y$ , 也就是说要强制走到$(x,y)$这个决策点,且该决策点在$y = x$的上方。

　我们将整个问题划分成两个部分，从$(0,0)$走到$(x,y)$，还有从$(x,y)$走到$(n,n)$。

　也就是说$(i,j)$可以走到$(i+1,j) $当且仅当$(i < j)$成立，也可以走到$(i+1,k)$其中$k>j$。

　对于走到$(i+1,k)$的路径可以看做先走到$(i,k)$再向右走到$(i+1,k)$的一条路径。

　所以，这样的走法，等价于从$(0,0)$走到$(x,y)$不经过$y = x$下方的方案数。

　同理，从$(x,y)$走到$(n,n)$的不能经过$y = x$下方和没有到达$(n,n)$，不能到达$y = n$.

　所以，$(x,y)$走到$(n-1,n-1)$的不能经过$y = x$下方的方案数。

　　

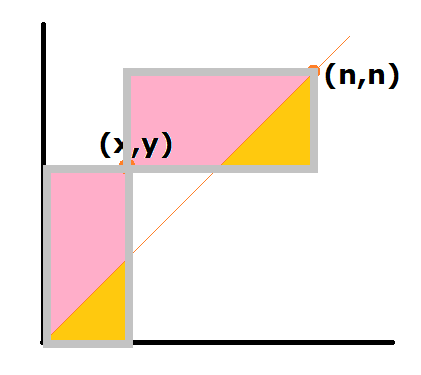
　此时的答案为​​$(\binom {x+y-2} {x-1} - \binom {x+y-2}{x-2})(\binom {2n-x-y}{n-x} - \binom {2n-x-y}{n-x+1})$

　如果$x > y$，根据对称性(将图像翻转$180°$仍然满足性质)，所以直接将$x  = n+1-x , y = n+1-y$，即可。

　对称性的原因是$x < y$考虑的信息是小于$x$ 的所有位置必须都小于$y$，否则不符合条件。

　如果$x > y$那么就是大于$x$的所有位置必须都大于$y$，否则不符合条件。

　所以本题最终复杂度为$O(n + T)$　

#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define REP(i,s,t) for(int i=s;i<=t;i++)
using namespace std;
const int Mod=1e9+,maxn=2e7+;
int fac[maxn],finv[maxn],inv[maxn];
int C(int n,int m){return 1ll*fac[n]*finv[m]%Mod*finv[n-m]%Mod;}
int main(){
#ifdef LOCAL
    freopen("tg1.in","r",stdin);
    freopen("ans.out","w",stdout);
#endif
    ios::sync_with_stdio(false);
    cin.tie();
    cout.tie();
    inv[]=; fac[]=finv[]=;
    REP(i,,2e7) inv[i]=1ll*(Mod-Mod/i)*inv[Mod%i]%Mod;
    REP(i,,2e7) fac[i]=1ll*i*fac[i-]%Mod;
    REP(i,,2e7) finv[i]=1ll*inv[i]*finv[i-]%Mod;
    int t; cin>>t;
    while(t--){
        int n,x,y; cin>>n>>x>>y;
        if(y<x) y=n+-y,x=n+-x;
        cout<<1ll*(C(x+y-,x-)-C(x+y-,x-)+Mod)*(C(n*-x-y,n-x)-C(n*-x-y,n-x+)+Mod)%Mod<<'\n';
    }
    return ;
}

tg.cpp