[ZJOI2007]捉迷藏 (线段树,括号序列)

大意: 给定树, 要求维护一个点集, 支持删点添点, 询问点集直径.

本题做法比较多.

一个显然的做法是, 线段树维护区间直径, 然后根据点集直径的性质, 合并后直径端点一定是四个端点其中两个, 枚举取最大即可.

如果用树剖求$lca$, 复杂度就为$O(nlog^2n)$.

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#define REP(i,a,n) for(int i=a;i<=n;++i)
#define pb push_back
#define lc (o<<1)
#define rc (lc|1)
#define mid ((l+r)>>1)
#define ls lc,l,mid
#define rs rc,mid+1,r
using namespace std;
const int N = 1e5+10;
int n, m, f[N];
int dep[N], sz[N], top[N], fa[N], son[N];
vector<int> g[N];
void dfs(int x, int f, int d) {
    fa[x]=f,dep[x]=d,sz[x]=1;
    for (int y:g[x]) if (y!=f) {
        dfs(y,x,d+1),sz[x]+=sz[y];
        if (sz[y]>sz[son[x]]) son[x]=y;
    }
}
void dfs(int x, int tf) {
    top[x]=tf;
    if (son[x]) dfs(son[x],tf);
    for (int y:g[x]) if (!top[y]) dfs(y,y);
}
int lca(int x, int y) {
    while (top[x]!=top[y]) {
        if (dep[top[x]]<dep[top[y]]) swap(x,y);
        x = fa[top[x]];
    }
    return dep[x]<dep[y]?x:y;
}
int dis(int x, int y) {
    if (!x||!y) return 0;
    return dep[x]+dep[y]-2*dep[lca(x,y)];
}
struct _ {
    int A,B,d;
    _ (int A=0,int B=0,int d=-1) :A(A),B(B),d(d) {}
    bool operator < (const _ &rhs) const {
        if (d!=rhs.d) return d<rhs.d;
        return !!A+!!B<!!rhs.A+!!rhs.B;
    }
    _ operator + (const _ &rhs) const {
        int c[4]={A,B,rhs.A,rhs.B};
        _ t;
        REP(i,0,3) REP(j,i+1,3) {
            _ tt(c[i],c[j],dis(c[i],c[j]));
            if (t<tt) t = tt;
        }
        return t;
    }
} tr[N<<2];
void update(int o, int l, int r, int x) {
    if (l==r) tr[o] = (f[l]^=1)?_(l):_();
    else mid>=x?update(ls,x):update(rs,x),tr[o]=tr[lc]+tr[rc];
}
void build(int o, int l, int r) {
    if (l==r) f[l] = 1, tr[o] = _(l);
    else build(ls),build(rs),tr[o]=tr[lc]+tr[rc];
}
int main() {
    scanf("%d", &n);
    REP(i,2,n) {
        int u, v;
        scanf("%d%d", &u, &v);
        g[u].pb(v),g[v].pb(u);
    }
    dfs(1,0,0),dfs(1,1);
    build(1,1,n);
    int m;
    scanf("%d", &m);
    while (m--) {
        char op;
        int x;
        scanf(" %c", &op);
        if (op=='G') printf("%d\n", tr[1].d);
        else scanf("%d", &x),update(1,1,n,x);
    }
}

还有一种做法是利用括号序列.

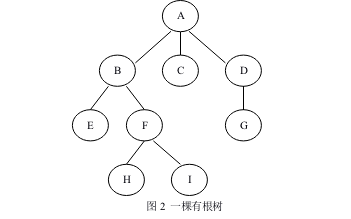
先序遍历后写成：$[A[B[E][F[H][I]]][C][D[G]]]$

考虑节点$E$和$G$, 取出括号编码 $][[][]]][][[$

删掉匹配的括号得到 $]][[$

意味着从$E$往上两步再往下两步就可以到达$G$.

所以树上一条路径可以表示为一段括号序列$S$, 然后$S$可以用一个二元组$S(a,b)$表示.

那么这个题需要动态维护$dis(S)=\{a+b|S'(a,b)$为$S$的子串, 且介于两黑点间$\}$.

对于括号序列$S$, 维护$7$个量$l,r,dis,L\_plus,L\_minus,R\_plus,R\_minus$

$l,r$为$S$的二元组, $dis$为黑点最大间距.

$L\_plus$为 $max\{l+r|S'$是$S$的前缀,且$S'$后为黑点$\}$.

$L\_minus$为 $max\{r-l|S'$是$S$的前缀,且$S'$后为黑点$\}$.

$R\_plus$为 $max\{l+r|S'$是$S$的后缀,且$S'$前为黑点$\}$.

$R\_minus$为 $max\{l-r|S'$是$S$的后缀,且$S'$前为黑点$\}$.

实现时把字母也添进括号序列, 用线段树维护每个量即可.

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <queue>
#define REP(i,a,n) for(int i=a;i<=n;++i)
#define pb push_back
#define lc (o<<1)
#define rc (lc|1)
#define mid ((l+r)>>1)
#define ls lc,l,mid
#define rs rc,mid+1,r
using namespace std;
const int N = 3e5+10, INF = 0x3f3f3f3f;
int n, m, sum, no[N], a[N], vis[N];
vector<int> g[N];
void dfs(int x, int f) {
	a[++*a] = -1, a[++*a] = x;
	for (int y:g[x]) if (y!=f) {
		dfs(y,x);
	}
	a[++*a] = -2;
}
struct _ {
	int l,r,dis,l_plus,l_minus,r_plus,r_minus;
	_ (int l=0,int r=0,int dis=0,int l_plus=0,int l_minus=0,int r_plus=0,int r_minus=0) : l(l),r(r),dis(dis),l_plus(l_plus),l_minus(l_minus),r_plus(r_plus),r_minus(r_minus) {}
	_ operator + (const _ &rhs) const {
		_ ret;
		ret.l = l+max(rhs.l-r,0);
		ret.r = rhs.r+max(r-rhs.l,0);
		ret.l_plus = max({l_plus,l+r+rhs.l_minus,l-r+rhs.l_plus});
		ret.l_minus = max(l_minus,rhs.l_minus+r-l);
		ret.r_plus = max({rhs.r_plus,r_plus-rhs.l+rhs.r,r_minus+rhs.l+rhs.r});
		ret.r_minus = max(rhs.r_minus,r_minus+rhs.l-rhs.r);
		ret.dis = max({dis,rhs.dis,r_plus+rhs.l_minus,r_minus+rhs.l_plus});
		return ret;
	}
} tr[N<<2];

void build(int o, int l, int r) {
	if (l==r) {
		if (a[l]>0) no[a[l]]=l,tr[o]=_(0,0,-INF);
		else tr[o]=_(a[l]==-2,a[l]==-1,-INF,-INF,-INF,-INF,-INF);
	}
	else build(ls),build(rs),tr[o]=tr[lc]+tr[rc];
}
void update(int o, int l, int r, int x) {
	if (l==r) {
		if (vis[l]) vis[l]=0,tr[o]=_(0,0,-INF);
		else vis[l]=1,tr[o]=_(0,0,-INF,-INF,-INF,-INF,-INF);
	}
	else mid>=x?update(ls,x):update(rs,x),tr[o]=tr[lc]+tr[rc];
}
int main() {
	scanf("%d", &n),sum=n;
	REP(i,2,n) {
		int u, v;
		scanf("%d%d", &u, &v);
		g[u].pb(v),g[v].pb(u);
	}
	dfs(1,0);
	build(1,1,*a);
	scanf("%d", &m);
	while (m--) {
		char op;
		int x;
		scanf(" %c", &op);
		if (op=='G') {
			int ans = tr[1].dis;
			if (sum==0) ans = -1;
			if (sum==1) ans = 0;
			printf("%d\n", ans);
		}
		else scanf("%d",&x),update(1,1,*a,no[x]);
	}
}