本地组策略功能中设置密码永不过期的时候发现功能置灰了，不能设置：

　

　　

　　

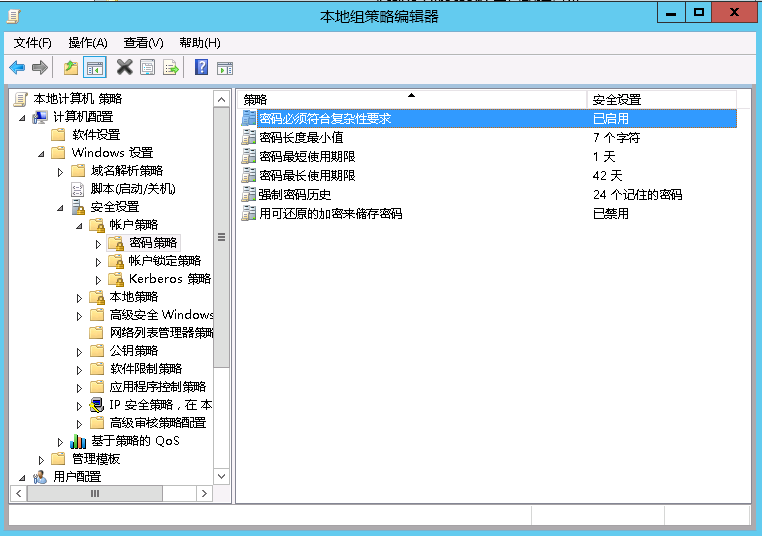
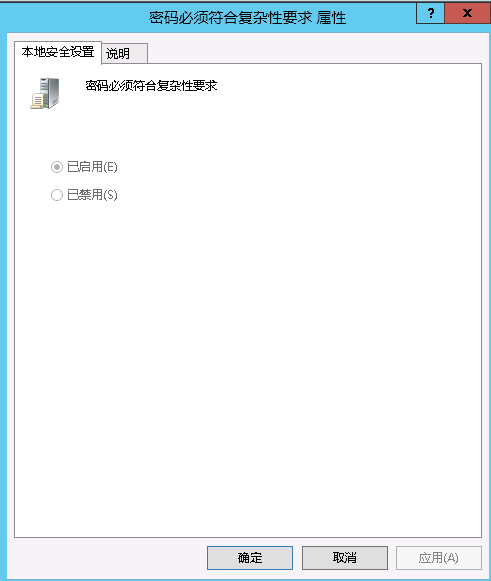
　　这是因为创建域后默认本地组策略功能会被转移到域组策略管理里面，所以我们可以去组策略管理器里去更改组策略，因为一般本地策略的优先级别最低，他会被域的密码策略立即覆盖！

　　运行"win+R"，输入“gpmc.msc”，在default domain policy里修改：

　　

　　

　　

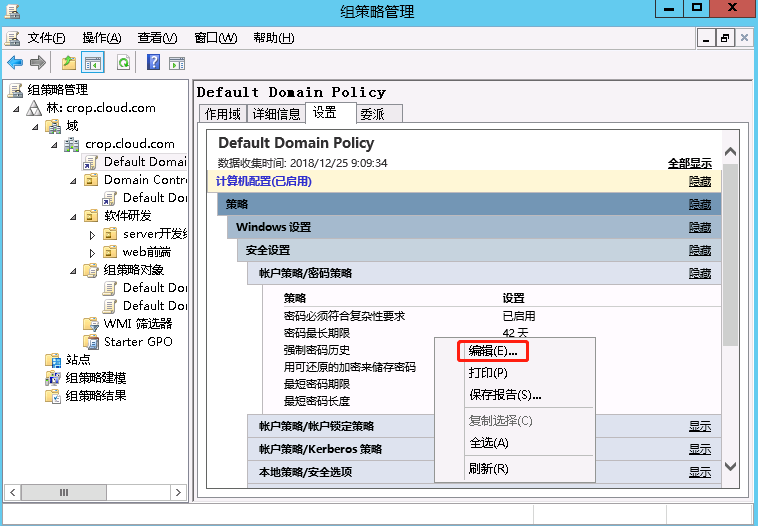
AD域环境取消密码复杂度和密码使用期限的更多相关文章

  1. AD域环境的搭建 基于Server 2008 R2

    AD(Active Directory)即活动目录,微软的基础件.微软的很多产品如:Exchange Server,Lync Server,SharePoint Server,Forefront Se ...

  2. AD域环境搭建

    1.安装Windows server服务器 我安装的是Windows server 2012 Standard x64 下载地址:https://pan.baidu.com/s/1dZ_B5JIEit ...

  3. Reporting Service服务SharePoint集成模式安装配置（1、虚拟机+ 2、AD域环境配置）

    研究 Reporting Service SharePoint 集成模式安装有一段时间,最初其实只是想知道Power View 技术是怎么回事,能实现什么效果.(当然也可以通过Excel 配置好 Po ...

  4. MySQL密码复杂度与密码过期策略介绍

    前言: 年底了,你的数据库是不是该巡检了?一般巡检都会关心密码安全问题,比如密码复杂度设置,是否有定期修改等.特别是进行等保评测时,评测机构会要求具备密码安全策略.其实 MySQL 系统本身可以设置密 ...

  5. 在权限受限制的AD域环境中部署SQL Server AlwaysOn高可用性

    最近在给一个客户部署基于微软TFS的软件生命周期管理平台时,客户要求数据库层实现高可用性,减少因数据库服务器故障影响软件开发进展. 客户现有域是一台搭建在Windows Server 2008上的级别 ...

  6. AD域渗透总结

    域渗透总结 学习并做了一段时间域网络渗透,给我直观的感受就是思路问题和耐心,这个不像技术研究,需要对一个点进行研究,而是遇到问题后要从多个方面思考,寻找"捷径"思路,只要思路正确, ...

  7. freeradius整合AD域作anyconncet认证服务器

    一.服务器要求 Radius服务器:centos6.6.hostname.selinux  disabled.stop iptables AD域服务器:Windows Server 2008 R2 E ...

  8. Windows中的DNS服务——正向解析&反向解析配置 分类： AD域 Windows服务 2015-07-16 20:21 19人阅读 评论(0) 收藏

    坚信并为之坚持是一切希望的原因. DNS服务是AD域不可或缺的一部分,我们在部署AD域环境时已经搭建了DNS服务(windows server 2008 R2域中的DC部署),但是DNS服务的作用还是 ...

  9. 在Windows Server 2012 R2域环境中禁用（取消）密码复杂策略

    windows server 2012域环境默认启用密码复杂策略,例如: 至少有六个字符长,包含以下四类字符中的三类字符:英文大写字母(A 到 Z),英文小写字母(a 到 z),10 个基本数字(0 ...

随机推荐

  1. Codeforces Round #456 (Div. 2) 912D D. Fishes

    题: OvO http://codeforces.com/contest/912/problem/D 解: 枚举每一条鱼,每放一条鱼,必然放到最优的位置,而最优位置即使钓上的概率最大的位置,即最多的r ...

  2. 传统Spring配置JTA 实现多数据源事务的统一管理

    分布式事务是指事务的参与者.支持事务的服务器.资源管理器以及事务管理器分别位于分布系统的不同节点之上,在两个或多个网络计算机资源上访问并且更新数据,将两个或多个网络计算机的数据进行的多次操作作为一个整 ...

  3. Hdu 2047 Zjnu Stadium(带权并查集)

    Zjnu Stadium Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total ...

  4. Navicat Premium 12破解版激活（全新注册机）

    使用打包下载就可以了 打包下载:(注册机有5.0和5.1用哪个看心情,我用的5.1) 连接:https://pan.baidu.com/s/1ARjFa2vEYxe9sljbrZR8fQ 提取码:lx ...

  5. The JAVA_HOME environment variable is not defined correctly的错误

    The JAVA_HOME environment variable is not defined correctlyThis environment variable is needed to ru ...

  6. spring事务之事务传播机制和隔离级别

    Spring事务传播行为 运用Spring事务,必须要深入理解它的传播机制,否则会遇到各种意想不到的坑,Spring定义了七种传播行为. public interface TransactionDef ...

  7. Sublime Text 3中配置Python3的开发环境

    在Tools-->Build System-->New Build System 之后弹出如下界面: 将其内容修改为 代码: { "cmd": ["D:/so ...

  8. POJ 2109 -- Power of Cryptography

    Power of Cryptography Time Limit: 1000MS   Memory Limit: 30000K Total Submissions: 26622   Accepted: ...

  9. 【MyBatis】从一千万记录中批量删除八百万条，耗时4m7s

    批量删除主要借助了MySql的limit函数,其次用了in删除. 代码如下: package com.hy.action; import java.io.Reader; import java.uti ...

  10. k8s应用01-----入门实例

    安装一个单机版的K8S 1.关闭防火墙firewalld2.安装etcd和kubernetesyum install -y etcd kubernetes(会自动安装docker)3.修改配置文件修改 ...