DS04--树

一、学习总结

1、树结构思维导图

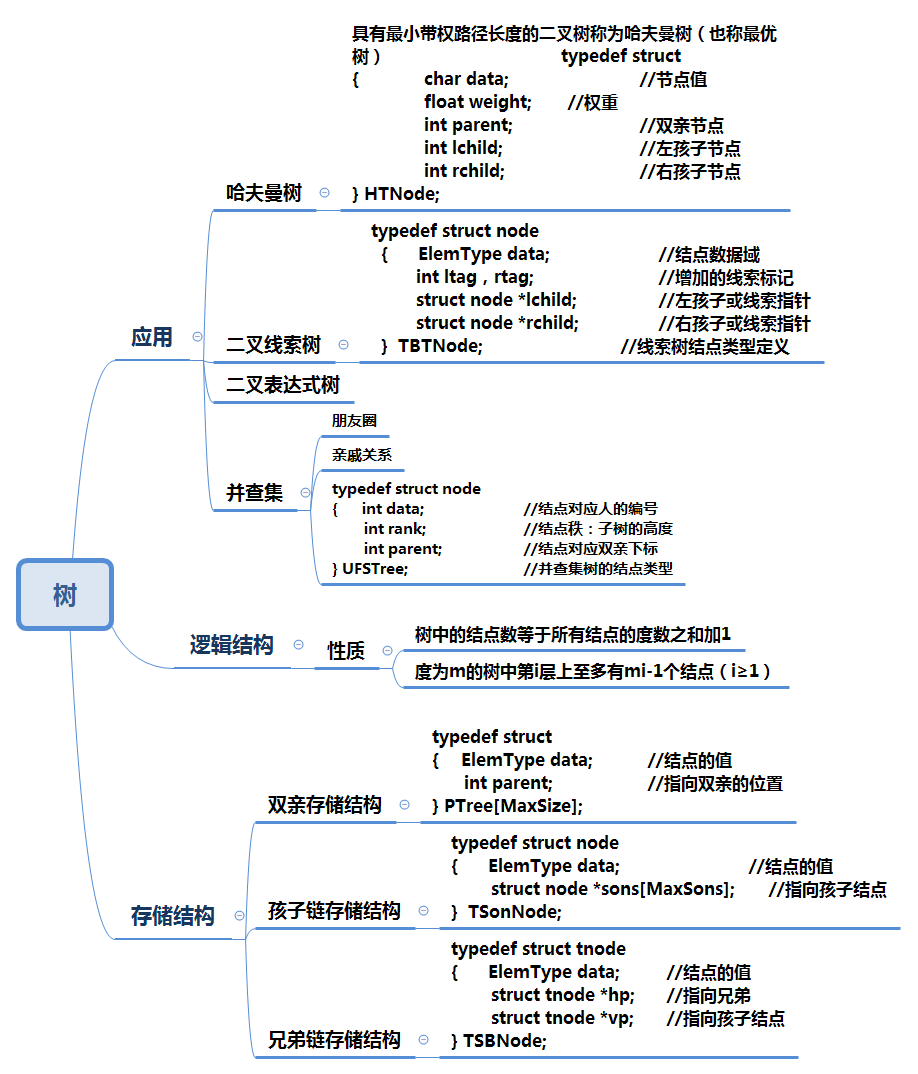
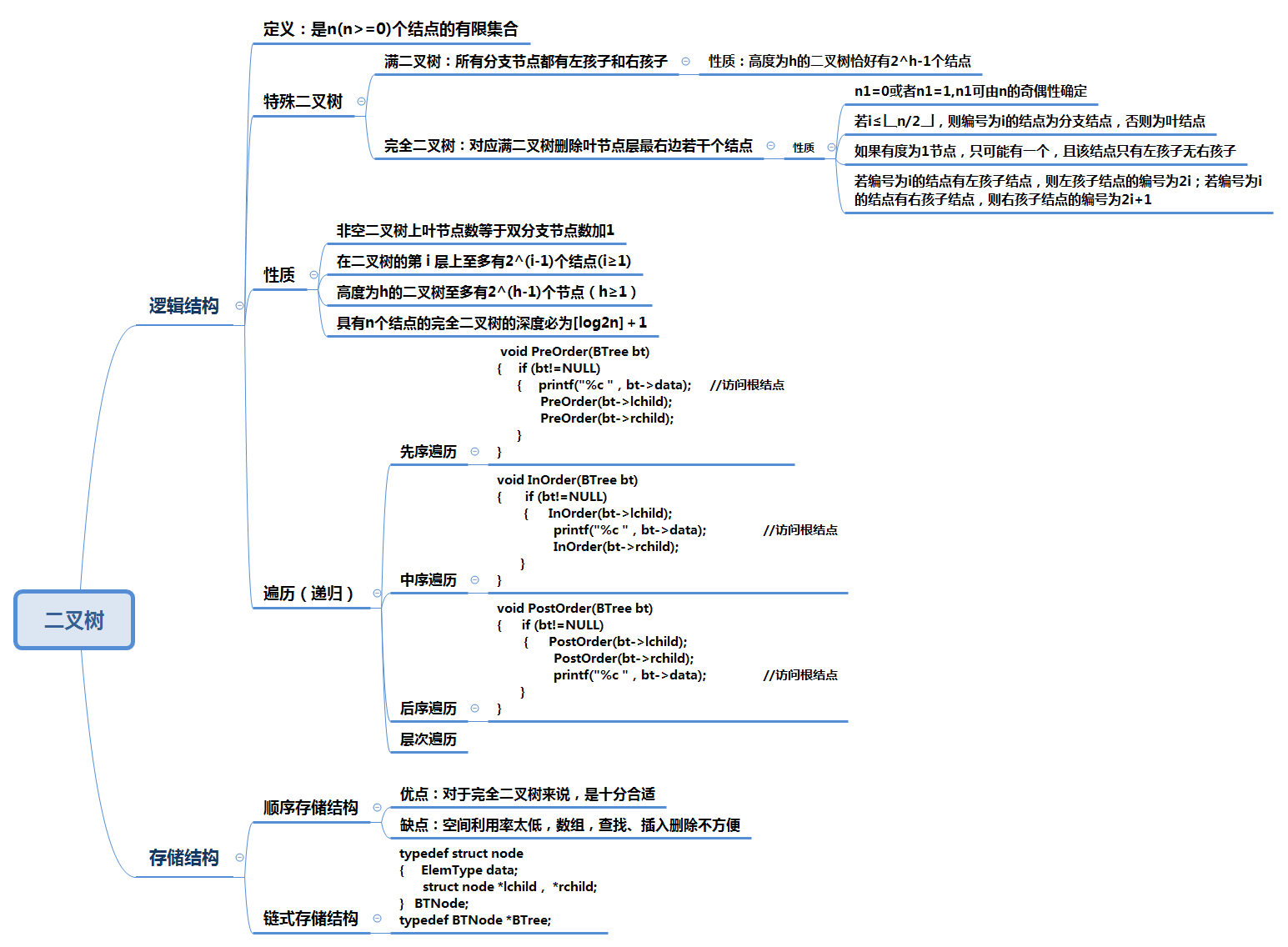
2、树结构学习体会

• 树这一节遇到最大的困难就是递归不能灵活的运用，总是想用链表那里的知识解决，做了一大堆，程序崩溃也找不到问题出在哪里。

二、PTA实验作业

题目1:表达式树

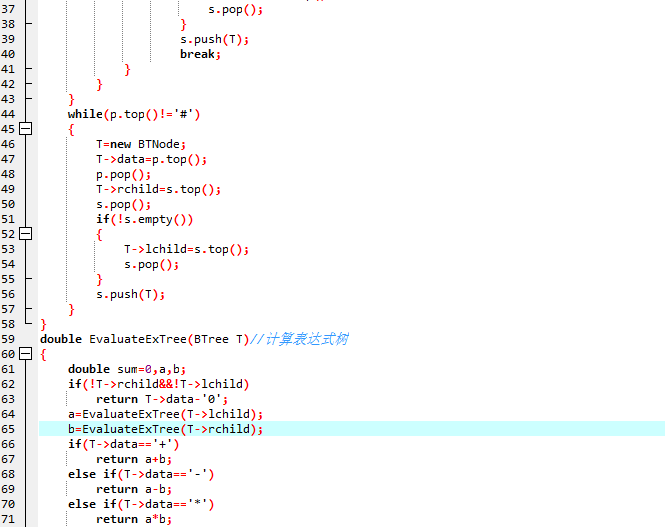
1、设计思路

void InitExpTree(BTree &T,string str)
{
    定义i做下标
	定义栈s用于存放树的节点数据
    定义字符栈p用来存放符号
    入栈#用作空栈标识

    while (str[i])
    {
        判断str[i]不是字符
        {
            创建树T并申请空间
            将str中的数据赋给树T
            左右子树初始化
            T中数据入栈s
        }
        否则
        {
            switch判断字符
            {
                "<"时
                    数据入栈p
                    i++;
                    break;
                "="时
                    p栈顶元素出栈;
                    i++;
                    break;
                ">"时
                    创建新节点T
                    将p栈顶元素赋给T
                    p栈顶元素出栈
                    将s的栈顶元素赋给T的右孩子
                    s栈顶元素出栈
                    if(s不为空)
                    {
                    	将s栈顶元素赋给左孩子
                    	s栈顶元素出栈
                    }
                    T元素入栈s
                    break;
            }
        }
    }
    while p栈顶元素不为'#'
    {
        创建新节点T
        将p栈顶元素赋给T
	    p栈顶元素出栈
        将s的栈顶元素赋给T的右孩子
        s栈顶元素出栈
        if(s不为空)
        {
           	将s栈顶元素赋给左孩子
           	s栈顶元素出栈
        }
        T元素入栈s
}
double EvaluateExTree(BTree T)
{
    定义a b两个运算变量
    判断T的左右孩子都不存在
        返回 T->data-'0';
    a=EvaluateExTree(T->lchild);
    b=EvaluateExTree(T->rchild);
    switch T此时的元素
    {
        '+'时
            返回a+b;
            break;
        '-'时
            返回a-b;
            break;
        '*'时
            返回a*b;
            break;
        '/'时
          	if(b==0)
               打印"divide 0 error!"
            否则返回a/b;
            break;
    }
}

2、代码截图

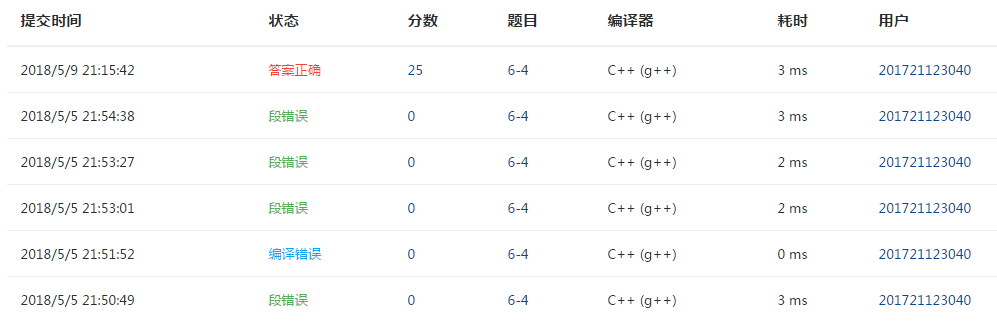
3、PTA提交列表说明

4、调试问题

- 段错误：在将栈s创建进树中是缺少情况建立左子树。添加当s不为空是，将s的栈顶元素赋给T的左子树

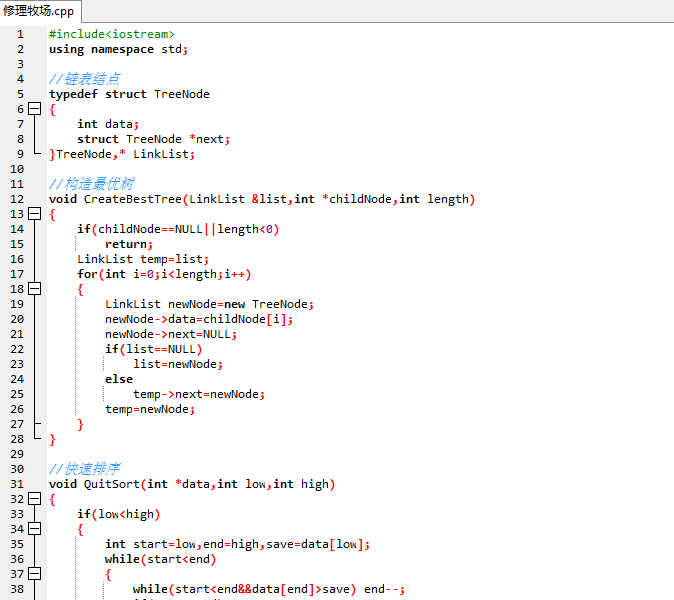
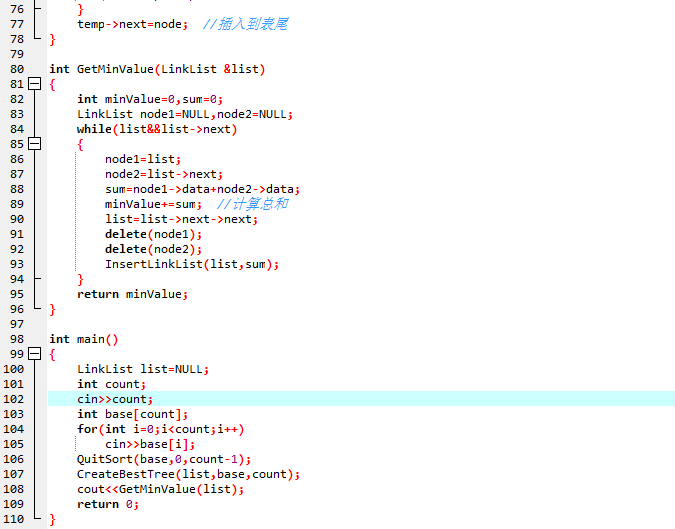
题目2:修理牧场

农夫要修理牧场的一段栅栏，他测量了栅栏，发现需要N块木头，每块木头长度为整数Li个长度单位，于是他购买了一条很长的、能锯成N块的木头，即该木头的长度是L​i​​ 的总和。但是农夫自己没有锯子，请人锯木的酬金跟这段木头的长度成正比。为简单起见，不妨就设酬金等于所锯木头的长度。例如，要将长度为20的木头锯成长度为8、7和5的三段，第一次锯木头花费20，将木头锯成12和8；第二次锯木头花费12，将长度为12的木头锯成7和5，总花费为32。如果第一次将木头锯成15和5，则第二次锯木头花费15，总花费为35（大于32）。

1、代码截图

2、PTA提交列表说明

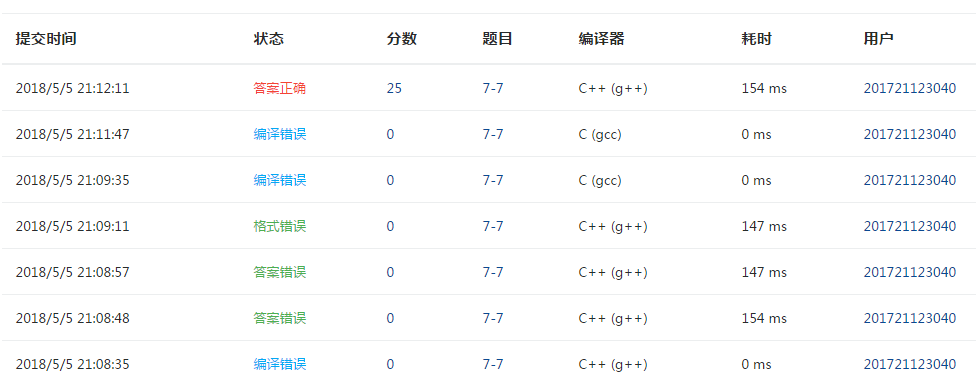
3、调试问题

- 哈夫曼树建不出来：这道题明显是用哈夫曼树，编写了很久但一直不能用树的结构写出来。最后用了链表做了出来。遇到的问题不算大。但是还是很可惜

- 编译错误 ：在释放链表结点时，c++该用delete,我用了free

- 其他问题会在阅读代码那边详细讲

题目3:求二叉树高度

1、设计思路

定义左子树高度、右子树高度变量

递归调用算左子树、右子树高度
返回左右子树高度最大值加一

2、代码截图

3、PTA提交列表说明

4、调试问题

- 思路错误：第一次做的时候，并没有想到用递归做，后来看了陈越版的课本才会用了递归

三、截图本周题目集的PTA最后排名

1、PTA排名

2、我的得分

2.5分

四、 阅读代码

修理牧场优秀代码

1、代码

---------------------------------优先队列做法-------------------------------
#include <cstdio>
#include <queue>

using namespace std;

priority_queue<int, vector<int>, greater<int> > q;

int main() {
    int n, m;

    scanf( "%d", &n );

    for( int i = 0; i < n; i++ ) {
        scanf( "%d", &m );
        q.push( m );
    }

    int sum = 0;

    while( q.size() > 1 ) {
        int first = q.top();
        q.pop();

        int second = q.top();
        q.pop();

        sum += first + second;
        q.push( first + second );
    }

    printf( "%d\n", sum );

    return 0;
}

--------------------------数组做法---------------------------
# include <stdio.h>
# include <malloc.h>

int main ()
{
    int i, m, num, t;
    int val;
    int cost=0;

    scanf ("%d", &num);
    int *a=(int*)malloc(sizeof(int)*num);

    for (i=0;i<num;i++)
        scanf ("%d", &a[i]);
    while (i!=1)
    {
        m=i-1;
        for (int j=0;j<i;j++)
            for (int k=0;k<i; k++)
                if (a[j]>a[k])
                {
                    t=a[j];
                    a[j]=a[k];
                    a[k]=t;
                }
                //for (int z=0;z<i;z++)
                //  printf("%d ",a[z]);
                //printf ("\n");
                a[m-1]=a[m-1]+a[m];
                cost=cost+a[m-1];
                //printf("%d\n",a[m]);
                i--;
    }
    printf ("%d\n", cost);
    return 0;
}

学习内容：

优先队列：它的“优先”意指取队首元素时，有一定的选择性，即根据元素的属性选择某一项值最优的出队~

百度百科上这样描述的：

　　优先级队列 是不同于先进先出队列的另一种队列。每次从队列中取出的是具有最高优先权的元素

　　优先队列的类定义　　

　　优先队列是0个或多个元素的集合,每个元素都有一个优先权或值,对优先队列执行的操作有： 查找; 插入一个新元素; 删除.

在最小优先队列(min priorityq u e u e)中,查找操作用来搜索优先权最小的元素,删除操作用来删除该元素;对于最大优先队列(max priority queue),查找操作用来搜索优先权最大的元素,删除操作用来删除该元素.优先权队列中的元素可以有相同的优先权,查找与删除操作可根据任意优先权进行.

给出一行字符串，求出其原编码需要的编码长度和哈夫曼编码所需的长度，并求其比值

分析：根据哈夫曼生成树的生成过程可知，其生成树的权值是固定的而且这个值是最小的，而且其值根据生成树的顺序，我们可以找出规律而

不需要真的去生成一棵树然后再求出权值，其模拟过程为取出队列中权值最小的两个元素，将其值加入结果中，然后将这两个元素的权值求和

即得出其父节点的权值，将生成元素作为结点入队~~如此循环，直至取出队列中最后两个元素加入结果，实现代码如下：

#include<stdio.h>
#include<string.h>
#include<ctype.h>
#include<functional>
#include<queue>
using namespace std;
#define M 1000050
char str[M];
int list[27];
priority_queue< int,vector<int>,greater<int> >que;
int main()
{
    int ans,sum;
    int i,a,b,c;
    while(scanf("%s",str),strcmp(str,"END")){
        memset(list,0,sizeof(list));
        for(i=0;str[i];i++){
            if(isalpha(str[i]))
                list[str[i]-'A']++;
            else
                list[26]++;
        }
        sum=i*8;ans=i;c=0;
        for(i=0;i<27;i++){
            if(list[i]){
                que.push(list[i]);
                c++;
            }
        }
        if(c>1){ans=0;//注意只有一种字符的情况
            while(que.size()!=1){
                a=que.top();
                que.pop();
                b=que.top();
                que.pop();
                ans+=a+b;
                que.push(a+b);
            }
            while(!que.empty())//使用后清空队列
                que.pop();
        }
        printf("%d %d %.1f\n",sum,ans,1.0*sum/ans);
    }
    return 0;
}

五、代码Git提交记录截图