FFT模板 生成函数 原根 多项式求逆 多项式开根

FFT

 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<cstdio>
 #include<cmath>
 #include<algorithm>
 #define maxn 1000005
 using namespace std;
 inline int read() {
     int x=,f=;char ch=getchar();
     for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-;
     for(;isdigit(ch);ch=getchar()) x=x*+ch-'';
     return x*f;
 }
 double pi=acos(-1.0);
 struct complex {
     double x,y;
     complex (double xx=,double yy=) {x=xx;y=yy;}
     complex operator +(const complex b) const {return complex(x+b.x,y+b.y);}
     complex operator -(const complex b) const {return complex(x-b.x,y-b.y);}
     complex operator *(const complex b) const {return complex(x*b.x-y*b.y,x*b.y+y*b.x);}
 }a[maxn],b[maxn];
 int n,m;
 int limit=,l,pos[maxn];
 void FFT(complex *A,int tp) {
     for(int i=;i<limit;i++) if(i<pos[i]) swap(A[i],A[pos[i]]);
     for(int mid=;mid<limit;mid<<=) {
         complex wn(cos(pi/mid),tp*sin(pi/mid));
         for(int R=mid<<,j=;j<limit;j+=R) {
             complex w(,);
             for(int k=;k<mid;k++,w=w*wn) {
                 complex x=A[j+k],y=w*A[j+mid+k];
                 A[j+k]=x+y;
                 A[j+mid+k]=x-y;
             }
         }
     }
     return ;
 }
 int main() {
     n=read(),m=read();
     for(int i=;i<=n;i++) a[i].x=read();
     for(int i=;i<=m;i++) b[i].x=read();
     while(limit<=n+m) limit<<=,l++;
     for(int i=;i<limit;i++) pos[i]=(pos[i>>]>>)|((i&)<<(l-));
     FFT(a,);
     FFT(b,);
     for(int i=;i<limit;i++) a[i]=a[i]*b[i];
     FFT(a,-);
     for(int i=;i<=n+m;i++) printf("%d ",(int)(a[i].x/limit+0.5));
 }

FFT

 生成函数

小A有ai个价值为Ai的物品，小B有bi个价值为Ai的物品，求用两个组成价值为ci的方案数

生成函数可以解决上面的这个问题，构造两个多项式，第X的Ai次方项的系数表示价值为i的物品有多少个，对两个人分别构造，乘在一起的多项式就代表所有的方案数。

原根

定义P的原根为满足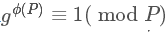的整数g。

NTT

 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<cstdio>
 #include<cmath>
 #include<algorithm>
 #define maxn 4000001
 #define mod 998244353
 #define ll long long
 using namespace std;
 inline int read() {
     int x=,f=;char ch=getchar();
     for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-;
     for(;isdigit(ch);ch=getchar()) x=x*+ch-'';
     return x*f;
 }
 ll a[maxn],b[maxn],pos[maxn];
 ll n,m,limit=,l,g=;
 ll power(ll x,ll y) {
     ll ans=;
     while(y) {
         if(y&) ans*=x,ans%=mod;
         x*=x,x%=mod;y>>=;
     }
     return ans;
 }
 void NTT(ll *A,int tp) {
     for(int i=;i<limit;i++) if(i<pos[i]) swap(A[i],A[pos[i]]);
     for(int mid=;mid<limit;mid<<=) {
         ll wn=power(g,(mod-)/(mid<<));
         if(tp==-) wn=power(wn,mod-);
         for(int j=;j<limit;j+=(mid<<)) {
             ll w=;
             for(int k=;k<mid;k++,w*=wn,w%=mod) {
                 ll x=A[j+k],y=w*A[j+mid+k];
                 A[j+k]=x+y;A[j+k]=(A[j+k]%mod+mod)%mod;
                 A[j+mid+k]=x-y;A[j+mid+k]=(A[j+mid+k]%mod+mod)%mod;
             }
         }
     }
     if(tp==-) {
         ll ny=power(limit,mod-);
         for(int i=;i<limit;i++) A[i]*=ny,A[i]=(A[i]%mod+mod)%mod;
     }
 }
 int main() {
     n=read(),m=read();
     for(int i=;i<=n;i++) a[i]=read();
     for(int i=;i<=m;i++) b[i]=read();
     while(limit<=n+m) limit<<=,l++;
     for(int i=;i<limit;i++) pos[i]=(pos[i>>]>>)|((i&)<<(l-));
     NTT(a,);
     NTT(b,);
     for(int i=;i<limit;i++) a[i]=a[i]*b[i],a[i]=(a[i]%mod+mod)%mod;
     NTT(a,-);
     for(int i=;i<=n+m;i++) printf("%lld ",a[i]);
 }

NTT

多项式求逆

 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<cstdio>
 #include<cmath>
 #include<algorithm>
 #define ll long long
 #define mod 998244353
 #define maxn 1000000
 using namespace std;
 inline int read() {
     int x=,f=;char ch=getchar();
     for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-;
     for(;isdigit(ch);ch=getchar()) x=x*+ch-'';
     return x*f;
 }
 ll g=,limit=,l,n;
 ll a[maxn],b[maxn],pos[maxn],c[maxn];
 ll power(ll x,ll y) {
     ll ans=;
     while(y) {
         if(y&) ans*=x,ans%=mod;
         x*=x,x%=mod;y>>=;
     }
     return ans;
 }
 void NTT(ll *A,int tp) {
     for(int i=;i<limit;i++) if(i<pos[i]) swap(A[i],A[pos[i]]);
     for(int mid=;mid<limit;mid<<=) {
         ll wn=power(g,(mod-)/(mid<<));
         if(tp==-) wn=power(wn,mod-);
         for(int j=;j<limit;j+=(mid<<)) {
             ll w=;
             for(int k=;k<mid;k++,w*=wn,w%=mod) {
                 ll x=A[j+k],y=w*A[j+mid+k]%mod;
                 A[j+k]=x+y;A[j+k]=(A[j+k]%mod+mod)%mod;
                 A[j+mid+k]=x-y;A[j+mid+k]=(A[j+mid+k]%mod+mod)%mod;
             }
         }
     }
     if(tp==-) {
         ll ny=power(limit,mod-);
         for(int i=;i<limit;i++) A[i]*=ny,A[i]=(A[i]%mod+mod)%mod;
     }
 }
 int d[maxn];
 void inv(int step,ll *A,ll *B) {
     if(step==) {B[]=power(A[],mod-);return;}
     inv((step+)>>,A,B);
     l=,limit=;
     while(limit<=(step<<)) limit<<=,l++;
     for(int i=;i<limit;i++) pos[i]=(pos[i>>]>>)|((i&)<<(l-));
     for(int i=;i<step;i++) c[i]=A[i];
     for(int i=step;i<limit;i++) c[i]=;
     NTT(c,);NTT(B,);
     for(int i=;i<limit;i++) B[i]=((2ll-c[i]*B[i]%mod)+mod)%mod*B[i]%mod;
     NTT(B,-);
     for(int i=step;i<limit;i++) B[i]=;
 }
 int main() {
     n=read();
     for(int i=;i<n;i++) a[i]=read();
     inv(n,a,b);
     for(int i=;i<n;i++) printf("%lld ",b[i]);
 }

多项式求逆

多项式开根

 void getsqr(ll *A,ll *B,ll len) {
     if(len==) {B[]=;return;}
     getsqr(A,B,(len+)>>);
     memset(invb,,sizeof(invb));
     getinv(B,invb,len);
     l=,limit=;
     while(limit<=(len<<)) limit<<=,l++;
     for(int i=;i<limit;i++) pos[i]=(pos[i>>]>>)|((i&)<<(l-));
     for(int i=;i<len;i++) c[i]=A[i];
     for(int i=len;i<limit;i++) c[i]=;
     NTT(invb,);NTT(c,);NTT(B,);
     for(int i=;i<limit;i++) {B[i]=((c[i]*invb[i]%mod)*inv2%mod+B[i]*inv2)%mod;}
     NTT(B,-);
     for(int i=len;i<limit;i++) B[i]=;
 }