vue 引入 mint-ui 简单使用

一 npm 方式

1，安装依赖 （已有项目）

如果想简单体验：基于vue-cli

/*

npm install vue -g

npm install vue-cli   -g   // -g 是否全局安装，如果不需要可不加

vue init webpack mint-pro

(一路回车默认即可)

*/

npm install -s mint-ui

2，main.js主函数配置

// 全局 mint-ui 引入
import Vue from 'vue'
import MintUI from 'mint-ui'
import 'mint-ui/lib/style.css'
import router from './router'
import App from './App'

Vue.use(MintUI);
Vue.config.productionTip = false

/* eslint-disable no-new */
new Vue({
  el: '#app',
  router,
  components: { App },
  template: '<App/>'
})

3，使用 app.vue

<template>
  <div id="app">
    <h2> hello mint-ui </h2>
    <button @click="handleToast">click me!</button>
    <button @click="handleIndictor">click me!</button>
    <router-view/>
  </div>
</template>

<script>
export default {
  name: 'App',
  methods: {
    handleToast () {
      this.$toast({
        message: '提示',
        position: 'middle',
        duration: 5000
      })
    },
    handleIndictor (){
      this.$indicator.open({
        text: 'loading',
        spinnerType: 'snake'
      });
      setTimeout(() => {
        this.$indicator.close()
      },2000);
    }
  }
}
</script>

4，npm run dev 预览结果

1）toast

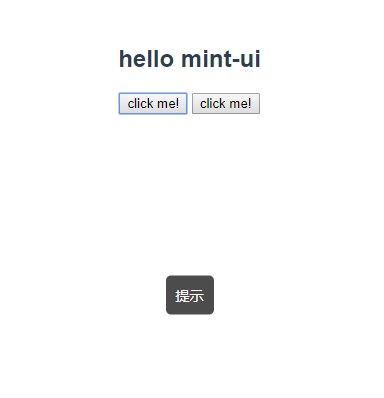
2) indicator

5, css 组件 直接把官方标签引入即可

<template>
  <div class="hello">
    <h3>css components</h3>
    <mt-header title="标题过长会隐藏后面的内容啊哈哈哈哈">
      <router-link to="/" slot="left">
        <mt-button icon="back">返回</mt-button>
      </router-link>
      <mt-button icon="more" slot="right"></mt-button>
    </mt-header>

    <h3>form components</h3>
    <mt-switch v-model="value">开关</mt-switch>

  </div>
</template>

<script>
  export default {
    name: 'HelloWorld',
    data() {
      return {
        value: false
      }
    }
  }
</script>

5.1 对应效果