线段树练习 3&&P3372 【模板】线段树 1

题目描述 Description

给你N个数，有两种操作：

1：给区间[a,b]的所有数增加X

2：询问区间[a,b]的数的和。

输入描述 Input Description

第一行一个正整数n，接下来n行n个整数，

再接下来一个正整数Q，每行表示操作的个数，

如果第一个数是1，后接3个正整数，

表示在区间[a,b]内每个数增加X,如果是2，

表示操作2询问区间[a,b]的和是多少。

pascal选手请不要使用readln读入

输出描述 Output Description

对于每个询问输出一行一个答案

样例输入 Sample Input

3

1

2

3

2

1 2 3 2

2 2 3

样例输出 Sample Output

9

数据范围及提示 Data Size & Hint

数据范围

1<=n<=200000

1<=q<=200000

-------------------------------------------------------------------------------------------------------------------------------------------------------------------------

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1：

5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4

输出样例#1：

11
8
20

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=1000，M<=10000

对于100%的数据：N<=100000，M<=100000

（数据已经过加强^_^，保证在int64/long long数据范围内）

样例说明：

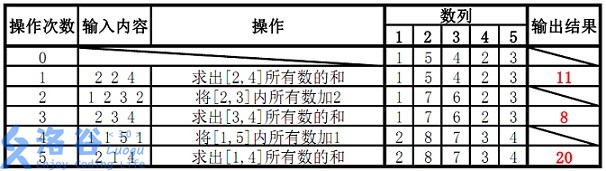
代码实现：

线段树练习 3：

 #include<cstdio>
 #include<iostream>
 #define LL long long
 using namespace std;
 LL n,m,a,b,c,d;
 struct nate{LL l,r,s,flag;}t[];
 void heritage(LL k){//标记传递。当使用某一区间时，把它的标记下传，并更改左右儿子的需求值。
     LL lson=k*,rson=k*+;
     t[lson].flag+=t[k].flag;
     t[lson].s+=(t[lson].r-t[lson].l+)*t[k].flag;
     t[rson].flag+=t[k].flag;
     t[rson].s+=(t[rson].r-t[rson].l+)*t[k].flag;
     t[k].flag=;
 }
 void make_tree(LL k,LL l,LL r){
     LL lson=k*,rson=k*+;
     t[k].l=l;t[k].r=r;
     if(l==r){
         scanf("%lld",&t[k].s);
         return;
     }
     LL mid=(l+r)/;
     make_tree(lson,l,mid);
     make_tree(rson,mid+,r);
     t[k].s=t[lson].s+t[rson].s;
 }
 void interval_change(LL k,LL l,LL r,LL v){
     LL lson=k*,rson=k*+;
     if(t[k].l==l&&t[k].r==r){
         t[k].flag+=v;
         t[k].s+=(t[k].r-t[k].l+)*v;
         return;
     }
     if(t[k].flag) heritage(k);
     LL mid=(t[k].l+t[k].r)/;
     if(l<=mid) interval_change(lson,l,min(r,mid),v);
     if(r>mid) interval_change(rson,max(l,mid+),r,v);
     t[k].s=t[lson].s+t[rson].s;
 }
 LL interval_query(LL k,LL l,LL r){
     LL lson=k*,rson=k*+;
     if(t[k].l==l&&t[k].r==r) return t[k].s;
     if(t[k].flag) heritage(k);
     long long mid=(t[k].l+t[k].r)/,ans=;
     if(l<=mid) ans+=interval_query(lson,l,min(r,mid));
     if(r>mid) ans+=interval_query(rson,max(l,mid+),r);
     return ans;
 }
 int main(){
     scanf("%lld",&n);
     make_tree(,,n);
     scanf("%lld",&m);
     for(int i=;i<=m;i++){
         scanf("%lld",&a);
         if(a==){
             scanf("%lld%lld%lld",&b,&c,&d);
             interval_change(,b,c,d);
         }
         if(a==){
             scanf("%lld%lld",&b,&c);
             printf("%lld\n",interval_query(,b,c));
         }
     }
     return ;
 }

【模板】线段树 1：

 #include<cstdio>
 #include<iostream>
 using namespace std;
 long long n,m,a,b,c,d;
 struct nate{long long l,r,s,flag;}t[];
 void heritage(long long k){
     long long lson=k*,rson=k*+;
     t[lson].flag+=t[k].flag;
     t[lson].s+=(t[lson].r-t[lson].l+)*t[k].flag;
     t[rson].flag+=t[k].flag;
     t[rson].s+=(t[rson].r-t[rson].l+)*t[k].flag;
     t[k].flag=;
 }
 void make_tree(long long k,long long l,long long r){
     long long lson=k*,rson=k*+;
     t[k].l=l;t[k].r=r;
     if(l==r){
         scanf("%lld",&t[k].s);
         return;
     }
     long long mid=(l+r)/;
     make_tree(lson,l,mid);
     make_tree(rson,mid+,r);
     t[k].s=t[lson].s+t[rson].s;
 }
 void interval_change(long long k,long long l,long long r,long long v){
     long long lson=k*,rson=k*+;
     if(t[k].l==l&&t[k].r==r){
         t[k].flag+=v;
         t[k].s+=(t[k].r-t[k].l+)*v;
         return;
     }
     if(t[k].flag) heritage(k);
     long long mid=(t[k].l+t[k].r)/;
     if(l<=mid) interval_change(lson,l,min(r,mid),v);
     if(r>mid) interval_change(rson,max(l,mid+),r,v);
     t[k].s=t[lson].s+t[rson].s;
 }
 long long interval_query(long long k,long long l,long long r){
     int lson=k*,rson=k*+;
     if(t[k].l==l&&t[k].r==r) return t[k].s;
     if(t[k].flag) heritage(k);
     long long mid=(t[k].l+t[k].r)/,ans=;
     if(l<=mid) ans+=interval_query(lson,l,min(r,mid));
     if(r>mid) ans+=interval_query(rson,max(l,mid+),r);
     return ans;
 }
 int main(){
     scanf("%lld%lld",&n,&m);
     make_tree(,,n);
     for(int i=;i<=m;i++){
         scanf("%lld",&a);
         if(a==){
             scanf("%lld%lld%lld",&b,&c,&d);
             interval_change(,b,c,d);
         }
         if(a==){
             scanf("%lld%lld",&b,&c);
             printf("%lld\n",interval_query(,b,c));
         }
     }
     return ;
 }

其实两个题几乎一样，也是因为这个“几乎”，我洛谷上得了遍零分。

题目来源：CODE[VS],洛谷