POI2014 FAR-FarmCraft

【Farm Craft】

【题目描述】

mhy住在一棵有n个点的树的1号结点上，每个结点上都有一个妹子。

mhy从自己家出发，去给每一个妹子都送一台电脑，每个妹子拿到电脑后就会开始安装zhx牌杀毒软件，第i个妹子安装时间为。

树上的每条边mhy能且仅能走两次，每次耗费1单位时间。mhy送完所有电脑后会回自己家里然后开始装zhx牌杀毒软件。

卸货和装电脑是不需要时间的。

求所有妹子和mhy都装好zhx牌杀毒软件的最短时间。

【Input】

第一行一个N，房屋数量

第二行N个数，C[i]

接下来的n - 1行表示相连接的房屋编号

【Output】

一个数字表示最少的时间

【Sample】

样例输入

6
1 8 9 6 3 2
1 3
2 3
3 4
4 5
4 6

样例输出

11

---

【Analyzation & Solution】

来看样例

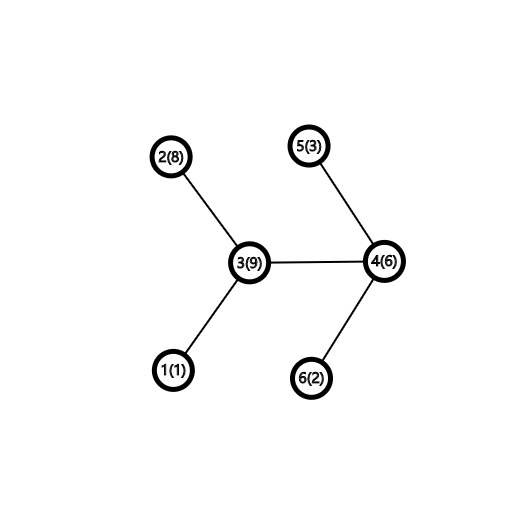
模拟一下

1 3 2 3 4 5 4 6 4 3 1

此时time为10

再加上最后回到出发点的自己安装软件所需时间1

答案是11

可见，上述模拟是通过先走大的再走小的

这样的话能保证安装同时进行

那么这个贪心究竟对不对呢？

我们来看这个图

仅仅是把节点5的权值更改为了50

远远大于节点3的9

那么此时显然我们要先遍历5号节点才是最优

如果按照上述贪心一定是不成立的

那怎么办呢？

咳咳

模拟样例的过程中发现

每个节点都有两种决策

这不禁让人联想到了树型DP

定义f[i]表示遍历以i为根的子树最短所用时间

size[i]即当前子树的大小（边数）

引用某大佬の证明

假设u节点有儿子x和y，则如果先走x的话u的时间就为max(f[x]+1,f[y]+2*size[x]+1)；
同理，先走 y 的话 u 的时间就为max(f[y]+1,f[x]+2*size[y]+1)，若先安装x合适，则必有2*size[x]+f[y]+1>2*size[y]+f[x]+1，即f[x]-2*size[y]<f[y]-2*size[x]。
既然这样，我们排序 f[i] - size[i] 即可。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;

inline int read(){
	int x = 0, w = 1;
	char ch = getchar();
	for(; ch > '9' || ch < '0'; ch = getchar()) if(ch == '-') w = -1;
	for(; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
	return x * w;
}

const int maxn = 500000+5;
int t, c[maxn], head[maxn], n, tot;
int f[maxn], size[maxn];
int q[maxn];
struct node{
    int to,nxt;
}e[maxn << 1];

inline bool cmp(int x, int y){
    return f[x] - 2 * size[x] > f[y] - 2 * size[y];
}

inline void add(int x, int y){
    e[++tot].to = y;
    e[tot].nxt = head[x];
    head[x] = tot;
}

inline void dfs(int u, int fa){
    int cnt=0, sum=1;
    if(u == 1) f[u]=0;
    else f[u] = c[u];
    size[u] = 1;
    for(int i = head[u]; i; i = e[i].nxt){
        int v = e[i].to;
        if(v == fa) continue;
        dfs(v,u);
        size[u] += size[v];
    }
    for(int i = head[u]; i; i = e[i].nxt)
        if(e[i].to != fa)
            q[++cnt] = e[i].to;
    sort(q + 1, q +1 + cnt, cmp);
    for(int i = 1; i <= cnt; i++){
        f[u] = max(f[u], f[q[i]] + sum);
        sum += 2 * size[q[i]];
    }
}

int main(){
    n = read();
    for(int i = 1; i <= n; i++) c[i] = read();
    for(int i = 1; i <= n - 1; i++){
        int x = read(), y = read();
        add(x, y);
        add(y, x);
    }
    dfs(1, -1);
    printf("%d", max(f[1], c[1] + 2 * (n - 1)));
    return 0;
}