BZOJ 1294 围豆豆 题解

题目

是不是平时在手机里玩吃豆豆游戏玩腻了呢？最近MOKIA手机上推出了一种新的围豆豆游戏，大家一起来试一试吧。

游戏的规则非常简单，在一个N×M的矩阵方格内分布着D颗豆子，每颗豆有不同的分值Vi。游戏者可以选择任意一个方格作为起始格，每次移动可以随意的走到相邻的四个格子，直到最终又回到起始格。最终游戏者的得分为所有被路径围住的豆豆的分值总和减去游戏者移动的步数。矩阵中某些格子内设有障碍物，任何时刻游戏者不能进入包含障碍物或豆子的格子。游戏者可能的最低得分为0，即什么都不做。

注意路径包围的概念，即某一颗豆在路径所形成的多边形（可能是含自交的复杂多边形）的内部。下面有两个例子：

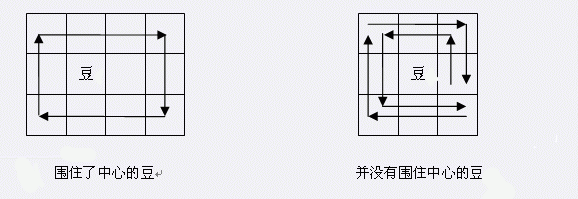
第一个例子中，豆在路径围成的矩形内部，所以豆被围住了。第二个例子中，虽然路径经过了豆的周围的8个格子，但是路径形成的多边形内部并不包含豆，所以没有围住豆子。

布布最近迷上了这款游戏，但是怎么玩都拿不了高分。聪明的你决定写一个程序来帮助他顺利通关。

输入格式

第一行两个整数\(N\)和\(M\)，为矩阵的边长。

第二行一个整数\(D\)，为豆子的总个数。

第三行包含\(D\)个整数\(V_1\)到\(V_D\)，分别为每颗豆子的分值。

接着\(N\)行有一个\(N \times M\)的字符矩阵来描述游戏矩阵状态，0表示空格，#表示障碍物。而数字1到9分别表示对应编号的豆子。

输出格式

仅包含一个整数，为最高可能获得的分值。

样例输入

3 8
3
30 -100 30
00000000
010203#0
00000000

样例输出

38

说明/提示

50%的数据满足\(1 \le D \le 3\)。

100%的数据满足\(1 \le D \le 9,1 \le N, M \le 10，-10000 \le V_i \le 10000\)。

题解

\(N,M\)的范围都很小,所以可以直接暴力广搜,但是保存状态不能直接用数组,处理起来会很麻烦,应该状态压缩.

我重点讲一下怎么判断一个点是否在多边形内:

先说结论,从某点向外做射线，若该射线与多边形相交了奇数次，该点就在该多边形的内部，否则在外部

下面证明

我们设想这个射线是从这个点出发的一条路径,在我们沿着这个路径走的过程中,可以得到以下结论:

由于射线无限长,而多边形有限,所以射线最后一次与多边形相交一定是从多边形内部交到外部,由此可得,倒数第二次相交(如果有的话)一定是从外部交到内部.

所以每交一次内外状态翻转,而最后的状态又是在外部,所以当交奇数次,最开始状态和最后的状态相反,即在内部,同理当交偶数次,最开始在外部.

这道题中规定从该点向右的射线为判定线,当你搜索路径奇数次相交于点\(i\)的判定线,点\(i\)在路径多边形内部,反之在外部.

当这个点的状态从在外部变成在内部,总分数加上这个点的分值;当这个点的状态从在内部变成在外部,总分数减去这个点的分值,注意搜索过程中每走一步总分值要减一.

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 15, M = 1050;
int n, m, d, f[N][N][M], vis[N][N], in[N][N][M], x[N], y[N], bean[N], ans, dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};
struct node {int x, y, status;};
queue<node> q;
void solve(int fx, int fy) {
    memset(f, 0, sizeof(f)), memset(in, 0, sizeof(in));
    f[fx][fy][0] = 0, q.push((node){fx, fy, 0});
    while (!q.empty()) {
        node now = q.front();
        q.pop();
        for (int k = 0; k < 4; k++) {
            int nx = now.x + dx[k], ny = now.y + dy[k];
            if (nx <= 0 || nx > n || ny <= 0 || ny > m || vis[nx][ny]) continue;
            int status = now.status, score = f[now.x][now.y][now.status] - 1; // 注意减去移动的1步
            if (k < 2) {  // k<2时,上下移动才可能穿过右射线
                for (int i = 1; i <= d; i++) {  //枚举豆子
                    if (x[i] != min(nx, now.x) || y[i] > ny) continue; //没穿过这个豆子的右射线 or 经过这个豆子的左边
                    if (status >> i - 1 & 1) score -= bean[i];
                    else score += bean[i];
                    status ^= (1 << (i - 1));  //改变经过次数奇偶性
                }
            }
            if (!in[nx][ny][status])
                in[nx][ny][status]=1, f[nx][ny][status] = score, q.push((node){nx, ny, status});
        }
    }
    for (int i = 0; i < (1 << d); i++)
        if (in[fx][fy][i]) ans = max(ans, f[fx][fy][i]);
}
int main() {
    scanf("%d%d%d", &n, &m, &d);
    for (int i = 1; i <= d; i++) scanf("%d", &bean[i]);
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++) {
            char c;
            scanf(" %c", &c);
            if (c == '#') vis[i][j] = -1;
            else x[c - '0'] = i, y[c - '0'] = j, vis[i][j] = c - '0';
        }
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            if (!vis[i][j]) solve(i, j);
    printf("%d\n", ans);
    return 0;
}