[MIT6.006] 1. Algorithmic Thinking, Peak Finding 算法思维，峰值寻找

[MIT6.006] 系列笔记将记录我观看《MIT6.006 Introduction to Algorithms, Fall 2011》的课程内容和一些自己补充扩展的知识点。该课程主要介绍了一些基础的算法，课程主要内容分为以下八个模块：

模块	例子
Algorithmic Thinking 算法思维	Peak Finding 峰值寻找
Sorting & trees 排序和树	Event Simulation 事务模拟
Hashing 哈希	Genome Comparison 基因组对比
Numerics 数值	RSA Encryption RSA加密
Graphs 图	Rubiks Cube 魔方
Shorest Paths 最短路径	Caltech -> MIT
Dynamic Programming 动态规划	Image Compression 图片压缩
Advanced Topics 高级主题

1. Algorithmic Thinking, Peak Finding 算法思维，峰值寻找

假设有一个如下图的一维数列，格子下的数字代表它们的索引位置，位置2为峰值peak，b必须满足：b≥a和b≤c。如果位置9为峰值，i≥h。这里是含有‘等于’是因为峰值寻找是建立“任何数列都存在峰值”的假设上。

直接采用最简单且最直接的峰值寻找方式，它的时间复杂度是ο(n)。为了实现更快的查询方法，我们可以采用二分查找（Binary Search）的思想，如下图所示：

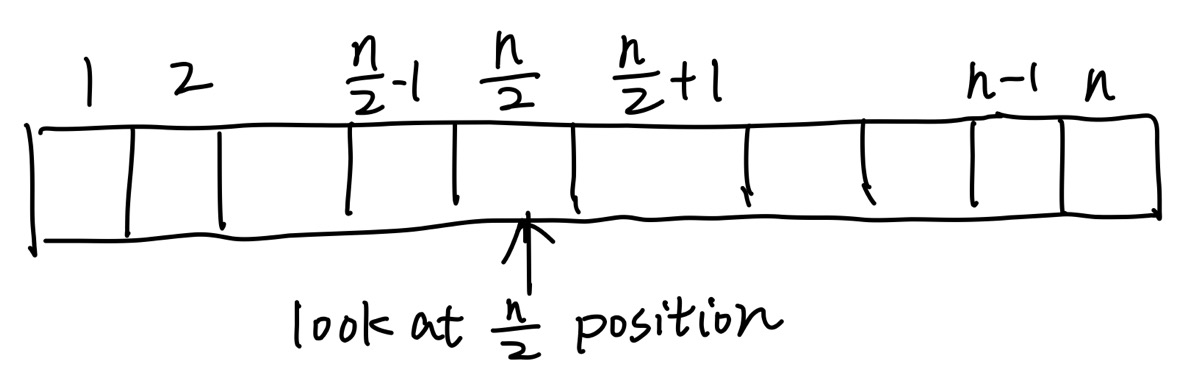
二分寻找峰值法主要步骤（假设上图数列为a，长度为n）：

• 先找到中间位置的数值a[n/2];
• if a[n/2]<a[n/2 - 1]，则在左边1至n/2 - 1的元素中寻找峰值;
• else if a[n/2]<a[n/2 + 1]，则在右边n/2 + 1至n的元素中寻找峰值;
• else: n/2位置上的元素是峰值。

二分峰值寻找法的时间复杂度是ο(log₂n)。跟二分法类似思路的时间复杂度常与log₂n挂钩。

假设有一个如下图的二维网格图，如果a≥b, a≥d, a≥c, a≥e，则a是2D-peak。

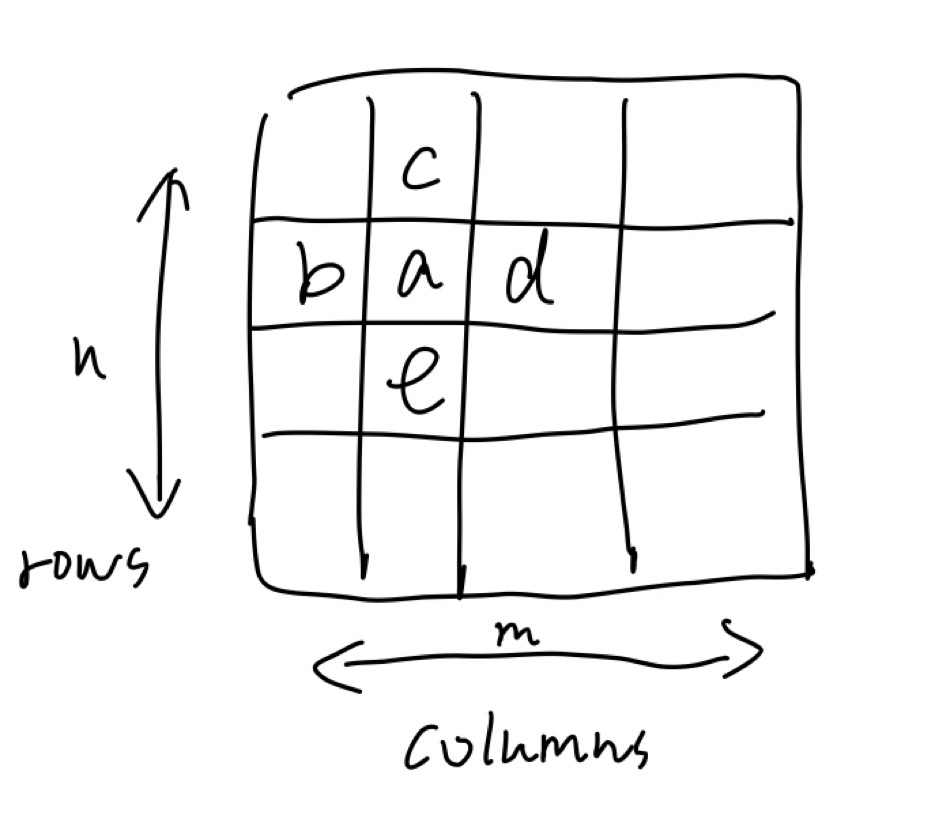
如果采用如下图所示的贪心算法，它的时间复杂度是ο(nm)。

而另一种方法是加入了二分查找思路去做：

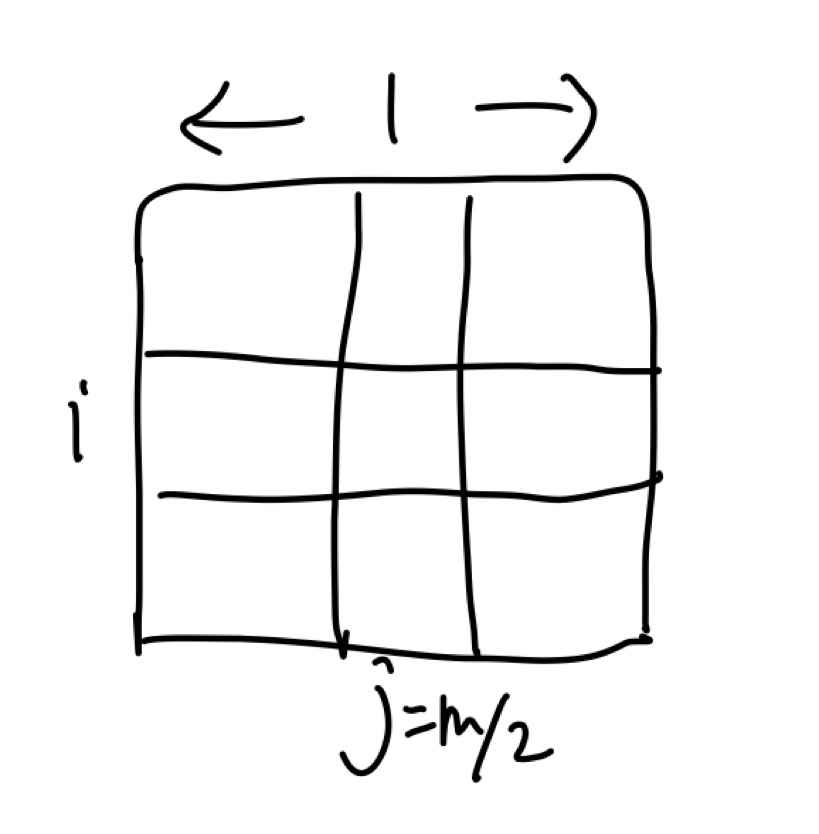
如上图所示：

• 首先，选中间列 j=m/2;
• 遍历列j的所有元素，找到列j的全局最大值val(i, j);
• 对比val(i, j-1), val(i, j), val(i, j+1);\
• 如果val(i, j-1) > val(i, j)，选择左边列继续重复以上步骤。相似地，如果val(i, j+1) > val(i, j)，选择右边列重复上面步骤。如果val(i, j)≥val(i, j-1)和val(i, j+1)，则val(i,j )就是2D-peak。

二分查找2D峰值的时间复杂度是ο(nlog₂m)，即在行(n)上寻找最大值 * 在列(m)上进行二分查找。