Java冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序

冒泡排序

  冒泡排序是一种简单的排序算法。它重复地走访过要排序地数列，一次比较两个元素，如果它们地顺序错误就把它们交换过来。走访数列地工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法地名字由来是因为越小地元素会经由交换慢慢“浮”到数列的顶端。

算法描述

• 比较相邻的元素。如果第一个比第二个大，就交换它们两个
• 对每一对相邻元素作同样的工作，从开始第一队到结尾的最后一对，这样在最后的元素应该会是最大的数
• 针对所有的元素重复以上的步骤，除了最后一个
• 从重步骤1~3，直到排序完成

动图描述

代码实现

	public static void bubbleSort(int[] a) {
		for(int i=0;i<a.length-1;i++) {
			for(int j=0;j<a.length-i-1;j++) {
				if(a[j]>a[j+1]) {
					int temp = a[j+1];
					a[j+1] = a[j];
					a[j] = temp;
				}
			}
		}
	}

选择排序

  选择排序(selection-sort)是一种简单直观的排序算法。它的工作原理：首先在末排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，在从剩余末排序元素中继续寻找最小（大）元素，然后放到已排序列的末尾。以此类推，直到所有元素均排序完毕。

算法描述

n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下：

• 初始状态：无序区为R[1..n]，有序区为空；
• 第i趟排序(i=1,2,3…n-1)开始时，当前有序区和无序区分别为R[1..i-1]和R(i..n）。该趟排序从当前无序区中-选出关键字最小的记录 R[k]，将它与无序区的第1个记录R交换，使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区；
• n-1趟结束，数组有序化了。

动图演示

代码实现

	public static void selectionSort(int a[]) {
		int minIndex,temp;
		for(int i=0;i<a.length-1;i++) {
			minIndex = i;
			for(int j=i+1;j<a.length;j++) {
				if(a[minIndex]>a[j]) {
					minIndex = j;
				}
			}
			temp = a[minIndex];
			a[minIndex] = a[i];
			a[i] = temp;
		}
	}

算法分析

  表现最稳定的排序算法之一，因为无论什么数据进去都是O(n2)的时间复杂度，所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。理论上讲，选择排序可能也是平时排序一般人想到的最多的排序方法了吧。

插入排序

  表现最稳定的排序算法之一，因为无论什么数据进去都是O(n2)的时间复杂度，所以用到它的时候，数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。理论上讲，选择排序可能也是平时排序一般人想到的最多的排序方法了吧。

算法描述

一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

• 从第一个元素开始，该元素可以认为已经被排序；
• 取出下一个元素，在已经排序的元素序列中从后向前扫描；
• 如果该元素（已排序）大于新元素，将该元素移到下一位置；
• 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
• 将新元素插入到该位置后；
• 重复步骤2~5。

动图演示

代码实现

      public static void InsertionSort(int a[]) {
		int preIndex,current;
		for(int i=1;i<a.length;i++) {
			preIndex = i - 1;
			current = a[i];
			while(preIndex>=0&&a[preIndex]>current) {
				a[preIndex+1] = a[preIndex];
				preIndex--;
			}
			a[preIndex+1] = current;

		}
	}

算法分析

  插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。

希尔排序

  1959年Shell发明，第一个突破O(n2)的排序算法，是简单插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。

  希尔本人给出的步长序列是n/2^k,比如n为16时,步长序列是{1,2,4,8}

算法描述

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：

• 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；
• 按增量序列个数k，对序列进行k 趟排序；
• 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

动态演示

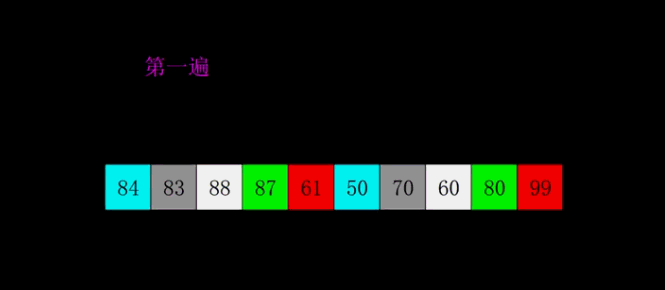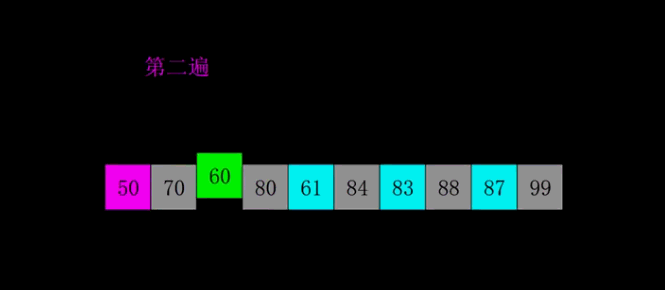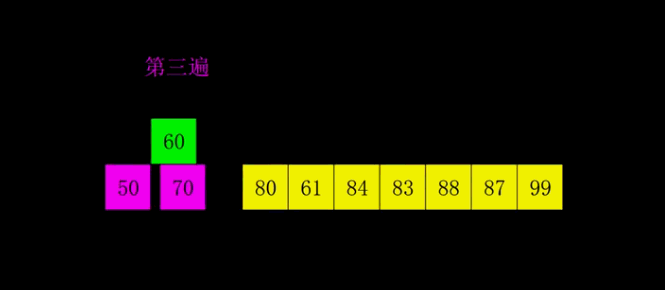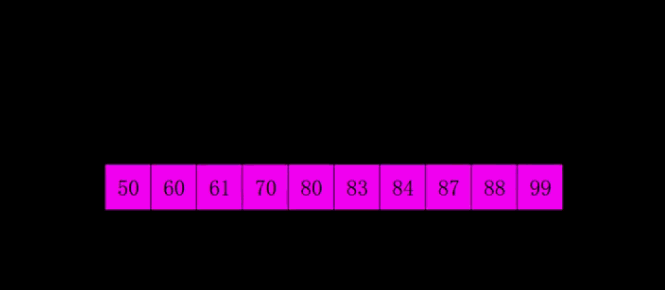
代码实现

      public static void ShellSort(int a[]) {
		for(int step = a.length/2;step>0;step=step/2) {
			for(int i=step;i<a.length;i++) {
				int value = a[i];
				int j;
				for(j=i-step;j>=0&&a[j]>value;j=j-step) {
					a[j+step] = a[j];
				} // 数组长度为奇数时，第一列中会出现3个元素
				a[j+step] = value;
			}
		}
	}

算法分析

  希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列，也可以动态的定义间隔序列。动态定义间隔序列的算法是《算法（第4版）》的合著者Robert Sedgewick提出的。　

归并排序

  归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。

算法描述

• 不断地将当前序列平均分割称2个子序列，直到不能再分割（序列中只剩1个元素）
• 不断地将2个子序列合并称一个有序序列
• 直到最终只剩下1个有序序列

动态演示

代码实现

      public static void Mergesort(int[] a, int low, int high) {
		int mid = (low + high) / 2;
		if (low < high) {
			Mergesort(a, low, mid);
			Mergesort(a, mid + 1, high);
			// 左右归并
			merge(a, low, mid, high);
		}
	}

	public static void merge(int[] a, int low, int mid, int high) {
		int[] temp = new int[high - low + 1];
		int i = low;
		int j = mid + 1;
		int k = 0;
		// 把较小的数先移到新数组中
		while (i <= mid && j <= high) {
			if (a[i] < a[j]) {
				temp[k++] = a[i++];
			} else {
				temp[k++] = a[j++];
			}
		}
		// 把左边剩余的数移入数组
		while (i <= mid) {
			temp[k++] = a[i++];
		}
		// 把右边边剩余的数移入数组
		while (j <= high) {
			temp[k++] = a[j++];
		}
		// 把新数组中的数覆盖nums数组
		for (int x = 0; x < temp.length; x++) {
			a[x + low] = temp[x];
		}
	}

算法分析

  归并排序是一种稳定的排序方法。和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是O(nlogn）的时间复杂度。代价是需要额外的内存空间。

快速排序

  快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。

算法描述

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

• 从数列中挑出一个元素，称为 “基准”（pivot）；
• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

动图演示

代码实现

public static void quickSort(int[] array) {
    int len;
    if(array == null|| (len = array.length) == 0|| len == 1) {
        return ;
    }
    sort(array, 0, len - 1);
}

public static void sort(int[] array, int left, int right) {
    if(left > right) {
        return;
    }
    // base中存放基准数
    int base = array[left];
    int i = left, j = right;
    while(i != j) {
        // 顺序很重要，先从右边开始往左找，直到找到比base值小的数
        while(array[j] >= base && i < j) {
            j--;
        }

        // 再从左往右边找，直到找到比base值大的数
        while(array[i] <= base && i < j) {
            i++;
        }

        // 上面的循环结束表示找到了位置或者(i>=j)了，交换两个数在数组中的位置
        if(i < j) {
            int tmp = array[i];
            array[i] = array[j];
            array[j] = tmp;
        }
    }

    // 将基准数放到中间的位置（基准数归位）
    array[left] = array[i];
    array[i] = base;

    // 递归，继续向基准的左右两边执行和上面同样的操作
    // i的索引处为上面已确定好的基准值的位置，无需再处理
    sort(array, left, i - 1);
    sort(array, i + 1, right);
}