AcWing243一个简单的整数问题2（树状数组+差分+前缀和规律）

题目地址：https://www.acwing.com/problem/content/244/

题目描述：

给定一个长度为N的数列A，以及M条指令，每条指令可能是以下两种之一：

1、“C l r d”，表示把 A[l],A[l+1],…,A[r] 都加上 d。

2、“Q l r”，表示询问 数列中第 l~r 个数的和。

对于每个询问，输出一个整数表示答案。

输入格式

第一行两个整数N,M。

第二行N个整数A[i]。

接下来M行表示M条指令，每条指令的格式如题目描述所示。

输出格式

对于每个询问，输出一个整数表示答案。

每个答案占一行。

数据范围

1≤N,M≤1e5,
|d|≤10000,
|A[i]|≤1000000000

题解：这是对树状数组的更深一步的扩展：区间加、区间求和。所以需要解决两个问题：区间加、区间和。区间加比较容易，直接差分就可以。至于区间和我们可以想办法求出原序列a的前缀和表示方法，b是原序列的差分数组

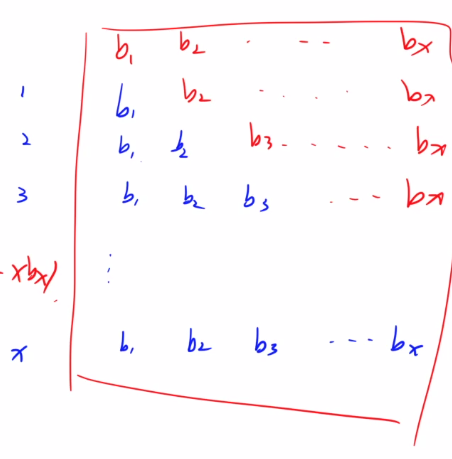
这张图片中的蓝色的，每一行蓝色的和都是一个元素a,分别表示a[1].....a[x].所以我们只需要求出a的前缀和，那么对于区间的和就显而易见了。至于图中的红色是一个填补的作用，我们可以知道a的前缀和就是蓝色+红色再减去红色。首先，蓝色+红色=a[x]*(x+1),而a[x]可以由差分数组b的前缀和求出。红色其实是i*b[i]的前缀和。所以a的前x的和S[x]=b[i]的前缀和*(x+1)-i*b[i]的前缀和。所以查询[l,r]=S[r]-S[l-1]

AC代码：

#include<iostream>
#include<cstring>
using namespace std;
const int N=1e5+;
#define lowbit(x) (x&(-x))
#define ll long long int
ll a[N]={},b[N]={},c[][N]={},n,m;

void add(int k,int x,ll d){
    while(x<=n){
        c[k][x]+=d;
        x+=lowbit(x);
    }
}

ll sum(int k,int x){
    ll sum=;
    while(x>){
        sum+=c[k][x];
        x-=lowbit(x);
    }
    return sum;
}

ll prefix_sum(int x){
    return sum(,x)*(x+)-sum(,x);
}

int main(){
    cin>>n>>m;
    memset(c,,sizeof(c));
    ll now=,x;
    for(int i=;i<=n;i++){
        cin>>x;
        a[i]=x-now;
        now=x;
    }
    for(int i=;i<=n;i++){
        add(,i,a[i]);//差分数组a[i]
        add(,i,i*a[i]);//差分数组i*a[i]
    }
    char ch;
    ll l,r,d;
    while(m--){
        cin>>ch;
        if(ch=='C'){
            cin>>l>>r>>d;
            add(,l,d);
            add(,r+,-d);
            add(,l,l*d);
            add(,r+,(r+)*(-d));
        }
        else {
            cin>>l>>r;
            cout<<(prefix_sum(r)-prefix_sum(l-))<<endl;
        }
    }
    return ;
}

写于：2020/8/26 17:27