对Innodb中MVCC的理解

一、什么是MVCC

　　MVCC (Multiversion Concurrency Control) 中文全程叫多版本并发控制，是现代数据库（如MySql）引擎实现中常用的处理读写冲突的手段，目的在于提高数据库高并发场景下的吞吐性能。

　　MySQL的InnoDB存储引擎默认事务隔离级别是RR(可重复读)，是通过 "行级锁+MVCC"一起实现的，正常读的时候不加锁，写的时候加锁。而 MCVV 的实现依赖：隐藏字段、Read View、Undo log。

　　另外MVCC只在 Read Committed 和 Repeatable Read两个隔离级别下工作，其他两个隔离级别和MVCC不兼容：

• Read Uncommitted总是读取最新的记录行，不需要MVCC的支持；
• Serializable 则会对所有读取的记录行都加锁，单靠MVCC无法完成。

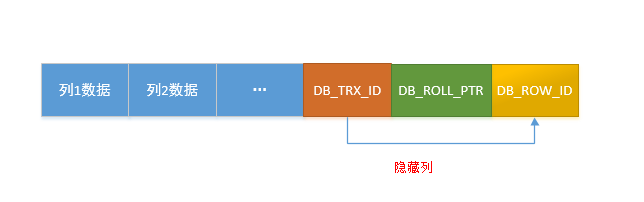
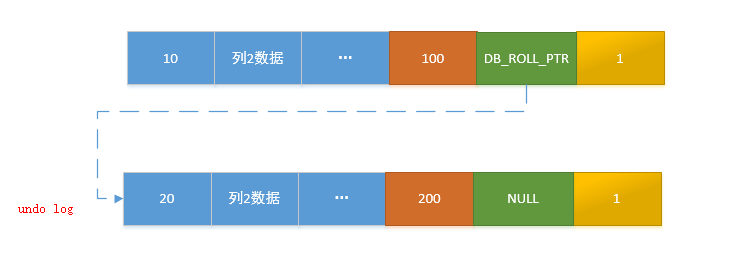
二、MVCC实现的核心知识点

1、事务版本号

　　每次事务开启前都会从数据库获得一个自增长的事务ID，可以从事务ID判断事务的执行先后顺序。

　　可以通过这样的命令来查看：select TRX_ID from INFORMATION_SCHEMA.INNODB_TRX;

 

2、隐藏字段（Innodb 为每行额外添加了3个字段，具体请参考官方文档）：

DB_TRX_ID：大小为6个字节。指插入或更新该行的最后一个事务的事务标识符，也就是事务ID。 此外，删除在内部被视为更新，在该更新中，该行中的特殊位被设置为将其标记为已删除。

DB_ROLL_PTR：大小为7个字节。表示指向该行回滚段的指针。 回滚指针指向写入回滚段的撤消日志记录。 如果行已更新，则撤消日志记录将包含在更新行之前重建行内容所必需的信息。

DB_ROW_ID：大小为6个字节。包含一个行ID，该行ID随着插入新行而单调增加。 如果InnoDB自动生成聚集索引，则该索引包含行ID值。 否则，DB_ROW_ID列不会出现在任何索引中。

3、Undo log

Undo log是InnoDB MVCC事务特性的重要组成部分。Undo log 主要用于记录数据被修改之前的日志，在表信息修改之前先会把数据拷贝到undo log 里，当事务进行回滚时可以通过undo log 里的日志进行数据还原。具体就不详细介绍了，请看考这两篇文档：https://dev.mysql.com/doc/refman/8.0/en/innodb-undo-logs.html http://mysql.taobao.org/monthly/2015/04/01/

4、read view

“InnoDB支持MVCC多版本，其中RC（Read Committed）和RR（Repeatable Read）隔离级别是利用consistent read view（一致读视图）方式支持的。所谓consistent read view就是在某一时刻给事务系统trx_sys打snapshot（快照），把当时trx_sys状态（包括活跃读写事务数组）记下来，之后的所有读操作根据其事务ID（即trx_id）与snapshot中的trx_sys的状态作比较，以此判断read view对于事务的可见性。

RR隔离级别（除了Gap锁之外）和RC隔离级别的差别是创建snapshot时机不同。 RR隔离级别是在事务开始时刻，确切地说是第一个读操作创建read view的；RC隔离级别是在语句开始时刻创建read view的（详见官方文档）。”

 

Read view中保存的trx_sys状态主要包括（以下字段解释来源于源码）：

trx_ids: 为活跃事务id列表，即Read View初始化时当前未提交的事务列表。所以当进行RR读的时候，trx_ids中的事务对于本事务是不可见的（除了自身事务，自身事务对于表的修改对于自己当然是可见的）。

low_limit_id: 当前最大的事务id + 1，事务id >= low_limit_id，对于当前Read View都是不可见的。理解起来就是在创建Read View视图的时候，之后创建的事务对于该事务肯定是不可见的。

up_limit_id: 当前已经提交的事务id + 1，事务id < up_limit_id ，对于当前Read View都是可见的。 理解起来就是在创建Read View视图的时候，之前已经提交的事务对于该事务肯定是可见的。

creator_trx_id: 创建当前read view的事务版本号；

一旦一个Read View被创建，这三个参数将不再发生变化，理解这点很重要，其中low_limit_id 和 up_limit_id分别是 trx_Ids数组的上下界（注意：从单词上来区分的话很容易弄反）。

其他事务对当前事务的可见性判断如下：

　　

三、案例分析

下面通过案例来分析MVCC怎么实现一致性读取的。前期数据准备：

• 使用默认隔离级别RR；
• 创建一个表： create table test(id int AUTO_INCREMENT, score int, primary key(id)) AUTO_INCREMENT = 0;
• 假设当前事务id已经自增长到100；

步骤	事务1	事务2	事务3
1	begin;
2		begin;
3	insert into test(score) select 101; 此时事务ID为101
4		insert into test(score) select 102; 此时事务ID为102
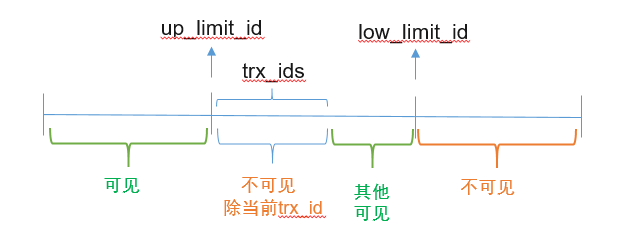
5	select * from test; +----+-------+ | id | score | +----+-------+ | 1 | 101 | +----+-------+ 此时就会创建read view： up_limit_id = 101 low_limit_id = 103 trx_ids为(101,102) 而101自身可见，102在活跃事务列表中不可见
6			insert into test(score) select 103; 此时事务ID为103
7			insert into test(score) select 104; 此时事务ID为104
8			nsert into test(score) select 105; 此时事务ID为105
9			select * from test; +----+-------+ | id | score | +----+-------+ | 3 | 103 | | 4 | 104 | | 5 | 105 | +----+-------+ 此时的up_limit_id=101，low_limit_id=106， trx_ids为（101, 102）， 而101和102在trx_ds列表中不可见
10		select * from test; +----+-------+ | id | score | +----+-------+ | 2 | 102 | | 3 | 103 | | 4 | 104 | | 5 | 105 | +----+-------+ 此时就会创建read view： up_limit_id=101， low_limit_id=106， trx_ids为（101, 102）， 102自身可见，101在活跃事务列表中不可见 而103、104、105不在trx_ids列表中所有可见
11	select * from test; +----+-------+ | id | score | +----+-------+ | 1 | 101 | | 3 | 103 | | 4 | 104 | | 5 | 105 | +----+-------+ 由于事务内read view不变 （与RC的区别就在这）， 此时的up_limit_id=101，low_limit_id=103， trx_ids为（101, 102）， 101自身可见，102在活跃事务列表中不可见 而>=103的都不可见

 

 

四、总结

　　1、MVCC主要靠Read view来实现一致性读，也就是快照读；底层是主要基于其中两个隐藏字段来实现（DB_TRX_ID、DB_ROLL_PTR）。这样可以使不同事务的读-写、写-读操作并发执行，从而提升系统性能。

　　2、Read view其中几个重要组成属性（trx_ids、low_limit_id、up_limit_id、creator_trx_id），一旦一个Read View被创建，这三个参数将不再发生变化；

　　3、MVCC只在 RC 和 RR两个隔离级别下工作， 它们的不同之处在于：

　　　　RR：read view是在first touch read时创建的，也就是执行事务中的第一条SELECT语句的瞬间，后续所有的SELECT都是复用这个read view，所以能保证每次读取的一致性（可重复读的语义）

　　　　RC：每次读取，都会创建一个新的read view。这样就能读取到其他事务已经COMMIT的内容。

　　所以对于InnoDB来说，RR虽然比RC隔离级别高，但是开销反而相对少。

　　补充：RU的实现就简单多了，不使用read view，也不需要管什么DB_TRX_ID和DB_ROLL_PTR，直接读取最新的record即可。

五、参考文献

http://mysql.taobao.org/monthly/2018/03/01/

https://github.com/twitter-forks/mysql/blob/master/storage/innobase/include/read0read.h#L124

https://dev.mysql.com/doc/refman/8.0/en/innodb-consistent-read.html