5.20 省选模拟赛 求和 组合数的性质 EGF CRT

LINK：求和

绝妙的一道题目。没做绝对亏了.

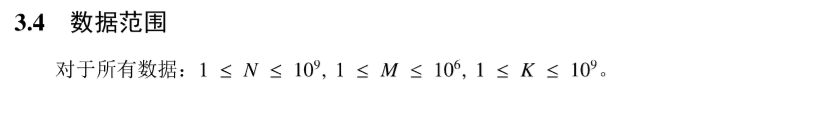
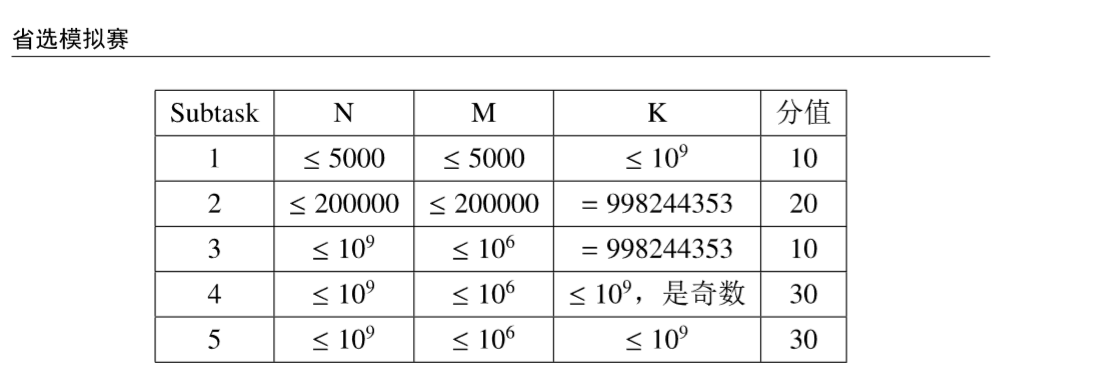
对于第一个subtask 考虑直接递推出组合数.

对于第二个subtask 考虑EGF 设两个EGF 都只含偶数项指标且系数为1的那种 一个到n一个到m 容易发现要求的东西为 两个EGF的卷积.

code score: 30

const int MAXN=50010,maxn=600010,G=3;
int n,m,mod,lim;
int c[2][MAXN];
int fac[maxn],A[maxn],B[maxn],inv[maxn],rev[maxn];
inline int mul(int a,int b){return (ll)a*b%mod;}
inline int add(int a,int b){return a+b>=mod?a+b-mod:a+b;}
inline int mus(int a,int b){return a-b<0?a-b+mod:a-b;}
inline int ksm(int b,int p)
{
	int cnt=1;
	while(p)
	{
		if(p&1)cnt=mul(cnt,b);
		b=mul(b,b);p=p>>1;
	}
	return cnt;
}
inline void NTT(int *a,int op)
{
	rep(0,lim-1,i)if(i<rev[i])swap(a[i],a[rev[i]]);
	for(int len=2;len<=lim;len=len<<1)
	{
		int mid=len>>1;
		int wn=ksm(G,op==1?(mod-1)/len:mod-1-(mod-1)/len);
		for(int j=0;j<lim;j+=len)
		{
			int d=1;
			for(int i=0;i<mid;++i)
			{
				int x=a[i+j],y=mul(a[i+j+mid],d);
				a[i+j]=add(x,y);a[i+j+mid]=mus(x,y);
				d=mul(d,wn);
			}
		}
	}
	if(op==-1)
	{
		int INV=ksm(lim,mod-2);
		rep(0,lim-1,i)a[i]=mul(a[i],INV);
	}
}
int main()
{
	freopen("c.in","r",stdin);
    freopen("c.out","w",stdout);
	get(n);get(m);get(mod);
	if(n&1)--n;if(m&1)--m;
	m=min(n,m);
	if(n<=5000&&m<=5000)
	{
		int ans=1;
		c[0][0]=1;
		rep(1,n,i)
		{
			rep(0,min(i,m),j)
			{
				if(!j)c[i&1][j]=1;
				else c[i&1][j]=add(c[(i-1)&1][j-1],c[(i-1)&1][j]);
				if(!(i&1)&&!(j&1))ans=add(ans,c[i&1][j]);
			}
		}
		put(ans);return 0;
	}
	if(n<=200000&&m<=200000&&mod==998244353)
	{
		fac[0]=1;
		rep(1,n,i)fac[i]=mul(fac[i-1],i);
		inv[n]=ksm(fac[n],mod-2);
		fep(n-1,0,i)inv[i]=mul(inv[i+1],i+1);
		for(int i=0;i<=n;i+=2)A[i]=inv[i];
		for(int i=0;i<=m;i+=2)B[i]=inv[i];
		lim=1;while(lim<=n+m)lim=lim<<1;
		rep(0,lim-1,i)rev[i]=rev[i>>1]>>1|((i&1)?lim>>1:0);
		NTT(A,1);NTT(B,1);
		rep(0,lim-1,i)A[i]=mul(A[i],B[i]);
		NTT(A,-1);int ans=0;
		rep(0,n,i)
		{
			if(i&1)continue;
			A[i]=mul(A[i],fac[i]);
			ans=add(ans,A[i]);
		}
		put(ans);
		return 0;
	}
}

我只能做这么多了。

剩下的考虑先推一些关于组合数的式子.

先考虑题解的绝妙式子吧：

将C(i,j)变成二项式定理展开后的式子 那么原式=

\(\sum_{j=0}^m\sum_{i=0}^n [x^j](x+1)^i,i\mod 2==0,j\mod 2==0\)

容易发现第二项是一个等比数列 可以先求一下和. 将n变成偶数。

设\(F(x)=\frac{(x+1)^{n+2}-1}{(x+1)^2-1}\)

所求就变成了\(\sum_{j=0}^m[j\mod 2==0][x^j]F(x)\)

(剩下需要 高深的东西了 二阶线性递推

源神给我讲了他的做法：

设\(g_j=\sum_{i=0}^nC(i,j)[i\mod 2==0],l_j=\sum_{i=0}^nC(i,j)[i\mod 2==1]\)

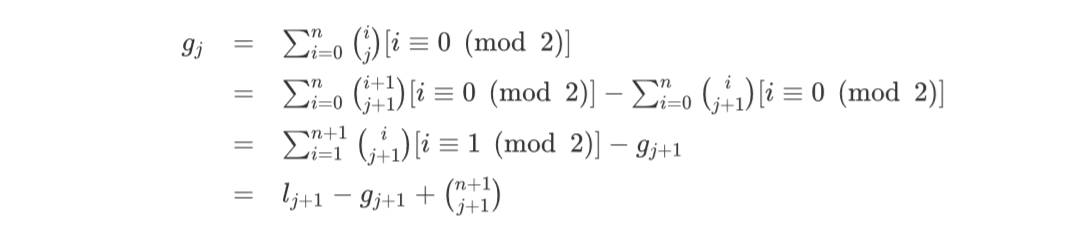
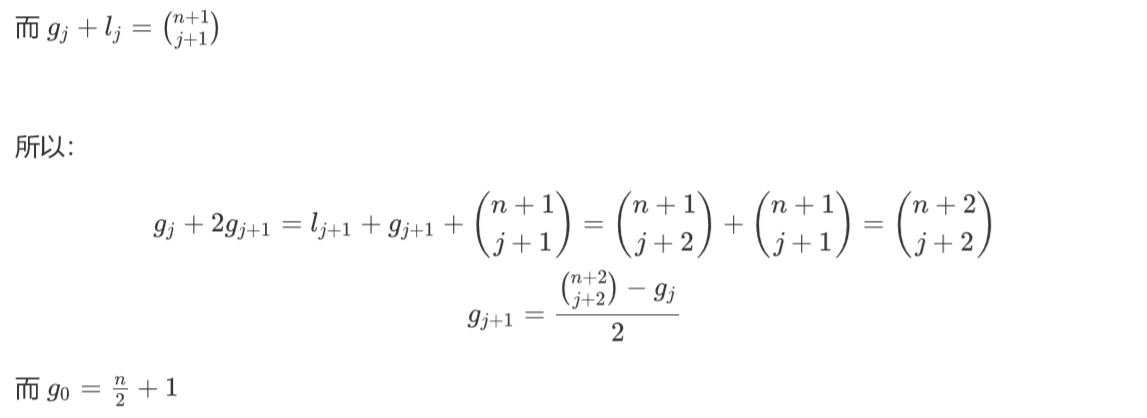
所以就可以递推出g了。

subtask3 很容易就解决了。(注意 组合数中有和mod相等的数的出现.

subtask4 可能不存在逆元了 通常都是 质因数分解然后CRT合并.

2的逆元还存在 所以还是可以递推的 复杂度 mlog^2 log很小 所以可以过。

subtask5 2的逆元可能不存在了 单独考虑模数2^b.

把递推式倒着写发现就没有除以2的问题了 考虑如何先求出gm.

做法如下：

code:

const int MAXN=1000050,maxn=50;
int n,m,B,ww,xx,yy,cnt,mod;
int w[maxn],p[maxn],f[maxn],v[maxn],phi[maxn],IN[maxn];
int C[MAXN],g[MAXN],G[MAXN];
inline void exgcd(int a,int b)
{
	if(!b){xx=1;yy=0;return;}
	exgcd(b,a%b);
	int zz=xx;xx=yy;yy=zz-a/b*yy;
}
inline int inv(int a,int b)
{
	exgcd(a,b);
	return (xx%b+b)%b;
}
inline int ksm(int b,int p,int mod)
{
	int cnt=1;
	while(p)
	{
		if(p&1)cnt=(ll)cnt*b%mod;
		b=(ll)b*b%mod;p=p>>1;
	}
	return cnt;
}
int main()
{
	freopen("c.in","r",stdin);
	freopen("c.out","w",stdout);
	get(n);get(m);get(mod);ww=mod;
	if(n&1)--n;if(m&1)--m;
	if(mod==1){puts("0");return 0;}
	m=min(n,m);
	for(int i=2;i*i<=ww;++i)
		if(ww%i==0)
		{
			p[++cnt]=i;
			w[cnt]=f[cnt]=1;v[cnt]=0;
			while(ww%i==0)
			{
				w[cnt]*=i;
				ww/=i;
			}
			phi[cnt]=w[cnt]/i*(i-1);
			IN[cnt]=inv(mod/w[cnt],w[cnt]);
		}
	if(ww>1)
	{
		p[++cnt]=ww;w[cnt]=ww;
		f[cnt]=1;v[cnt]=0;
		phi[cnt]=ww-1;
		IN[cnt]=inv(mod/w[cnt],w[cnt]);
	}
	C[0]=1;
	rep(1,min(n+2,m+32),i)
	{
		int ans=0;
		rep(1,cnt,j)
		{
			int w1=n+2-i+1;
			int w2=i;
			while(w1%p[j]==0)
			{
				++v[j];
				w1/=p[j];
			}
			while(w2%p[j]==0)
			{
				--v[j];
				w2/=p[j];
			}
			f[j]=(ll)f[j]*w1%w[j]*ksm(w2,phi[j]-1,w[j])%w[j];
			int v1=(ll)ksm(p[j],v[j],w[j])*f[j]%w[j];
			ans=(ans+(ll)IN[j]*v1%mod*(mod/w[j]))%mod;
		}
		C[i]=ans;
	}
	int w1=p[1]==2?mod/w[1]:mod;
	int ans=0;
	g[0]=n/2+1;ans=g[0]%=w1;
	int INV=inv(2,w1);
	rep(1,m,i)
	{
		g[i]=((ll)(C[i+1]-g[i-1])%w1*INV%w1+w1)%w1;
		if(!(i&1))ans=(ans+g[i])%w1;
	}
	if(p[1]==2)
	{
		int cc=w[1];
		while(cc!=1)
		{
			++B;
			cc=cc>>1;
		}
		cc=1;int ans1=0;
		rep(0,B-1,i)G[m]=(G[m]+(ll)cc*C[i+m+2])%w[1],cc=cc*(-2)%w[1];
		ans1=G[m];
		fep(m-1,0,i)
		{
			G[i]=(C[i+2]-(ll)2*G[i+1])%w[1];
			if(!(i&1))ans1=(ans1+G[i])%w[1];
		}
		//合并 ans1 ans
		int c1=inv(mod/w[1],w[1]);
		int c2=inv(mod/w1,w1);
		ans=((ll)ans*c2%mod*(mod/w1)%mod+(ll)ans1*c1%mod*(mod/w[1])%mod)%mod;
	}
	ans+=mod;ans%=mod;put(ans);
	return 0;
}