C++树——遍历二叉树

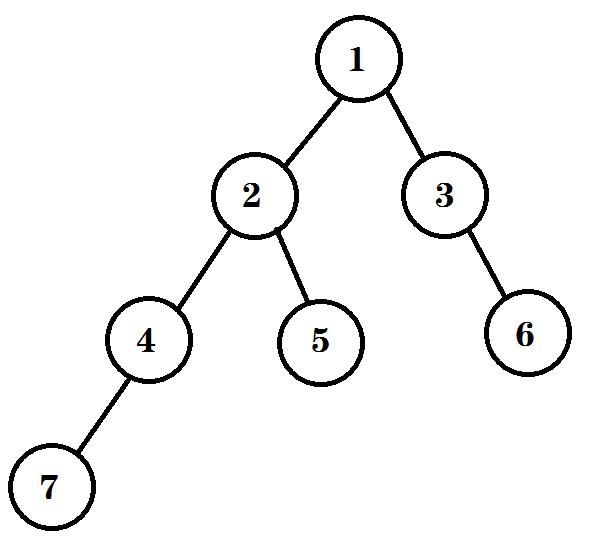
在讲遍历之前，我们要先创建一个树：

#include <iostream>
using namespace std;
typedef struct node;
typedef node *tree;

struct node{
    int data;               // 结点数值
    tree left,right;        // 左子树和右子树
};
tree bt;

遍历二叉树有三种方式：

先序遍历：

先序遍历的操作如下：

1. 访问根结点
2. 先序遍历左子树（递归）
3. 先序遍历右子树（递归）

二叉树bt的先序遍历结果：12347536

代码如下：

void preorder(tree bt){
    if (bt){                // 判断不为空二叉树
        cout << bt.data;
        preorder(bt.left);  // 递归遍历左子树
        preorder(bt.right); // 递归遍历右子树
    }
}

中序遍历：

中序遍历的操作如下：

1. 中序遍历左子树（递归）
2. 访问根结点
3. 中序遍历右子树（递归）

二叉树bt的中序遍历结果：7425136

代码如下：

void inorder(tree bt){
    if (bt){                // 判断不为空二叉树
        inorder(bt.left);   // 递归遍历左子树
        cout << bt.data;
        inorder(bt.right);  // 递归遍历右子树
    }
}

后序遍历：

后序遍历的操作如下：

1. 后序遍历左子树（递归）
2. 后序遍历右子树（递归）
3. 访问根结点

二叉树bt的后序遍历的结果：7452631

代码如下：

void postorder(tree bt){
    if (bt){                // 判断不为空二叉树
        postorder(bt.left);    // 递归遍历左子树
        postorder(bt.right); // 递归遍历右子树
        cout << bt.data;
    }
}

小结：我们使用递归的方式遍历了二叉树，大家仔细观察可以发现，先序遍历就是先访问根结点，再递归，中序遍历是把访问根结点放中间，后续遍历是最后访问。

补充知识：

表达式：a+b*c

表达式二叉树：

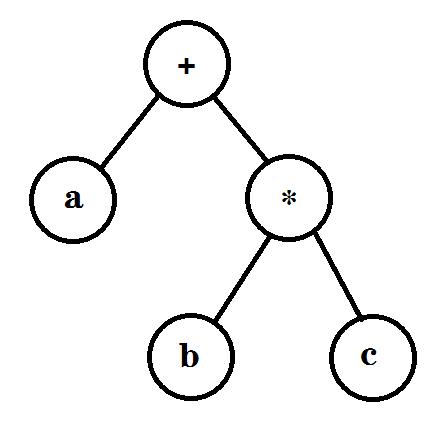
前缀表达式（波兰式）：+a*bc

中缀表达式：a+b*c/d

后缀表达式（逆波兰式）：abc*+

怎么将中缀表达式转换为前缀表达式或后缀表达式呢？只需像前序遍历和后序遍历一样遍历表达二叉树即可。