【赛时总结】◇赛时·VI◇ Atcoder ABC-104

◇赛时·VI◇ ABC-104

---

◆？？？

莫名爆炸……ABC都AK不了 QwQ

C题竟然沦落到卡数据的地步；D题没有思路，直接放弃 ⋋( ◕ ∧ ◕ )⋌

---

◆ 题目&解析

◇A题◇ Rated for Me +传送门+

• 【题意】

给出比赛的场次；将场次小于1200的编为"ABC"，场次大于等于1200小于2800的编为"ARC"，场次大于等于2800小于4208的编为"AGC"；输出编号。

• 【解析】

个人觉得不需要讲……题目读懂，if语句一写就好了……（萌新reader如果不太懂可以在文末邮箱email）

• 【源代码】

 /*Lucky_Glass*/
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 int main()
 {
     int n;scanf("%d",&n);
     if(n<) printf("ABC\n");
     else if(n<) printf("ARC\n");
     else printf("AGC\n");
     return ;
 }

◇B题◇  AcCepted +传送门+

• 【题意】

给出一个长度在4到10的字符串，一个字符串的结果为"AC"当且仅当 该字符串开头为大写A，从开头第3个字符到末尾第2个字符（包含）之间恰好存在一个大写C，除去‘A’、'C'两个字符，其余字符均为小写；否则结果为"WA"。输出对应字符串的结果。

• 【解析】

名副其实的英语阅读题……就因为一个题目没读懂WA了3遍 QwQ

先判断开头是否为A。定义bool变量F，标记从开头第3个字符到末尾第2个字符（包含）之间是否已经找到一个C，再扫描整个字符串，如果在从开头第3个字符到末尾第2个字符（包含）之外有大写字母（除了开头的A），则判为WA，若在正确区间内发现了C，就修改F为true，如果发现修改前F已经为true，说明C太多了，也判为WA。其余答案为AC。

• 【源代码】

 /*Lucky_Glass*/
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 char str[];
 int len;
 int main()
 {
     scanf("%s",str);
     len=strlen(str);
     if(str[]!='A') {printf("WA\n");return ;}
         bool F=false;
         for(int i=;i<len;i++)
             if('A'<=str[i] && str[i]<='Z')
             {
                 if(str[i]=='A' && i!=) {printf("WA\n");return ;}
                 if(str[i]=='C')
                     if(<=i && i<=len-)
                     {
                         if(F){printf("WA\n");return ;}
                         else F=true;
                     }
                 else {printf("WA\n");return ;}
                 if(str[i]!='A' && str[i]!='C') {printf("WA\n");return ;}
             }
         if(!F){printf("WA\n");return ;}
         printf("AC\n");
     return ;
 }

◇C题◇ All Green +传送门+

• 【题意】

有D种题，第i种题有 P_i 个，每个分值为 100*i ，若将第 i 种题全部做完，会额外奖励 C_i 分。求要得到至少 G 分最少需要做多少道题。保证有解，且 G 和 C_i 是100的倍数。

• 【解析】 Tab：下面讲的不是正解

沦落到只能卡数据……

看到这道题的第一想法就是背包，一个特别的多重背包。状态定义非常标准化，dp[i][j] 表示前 i 种题获得至少 j 分的最小做题数。转移方程也很寻常，只是加了一个做完一种题的额外分的特殊处理(感谢ywk童鞋，下面修改了一个错误 2018-08-06 10:52:17)：

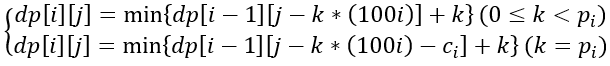
但是我们发现……题目的 G 竟然没有定义最大值，只说有解……

这就意味着dp[i][j]的第二维其实是会爆内存的。不可否认单纯的DP一定足够快，但是内存非常的感人。

但是我一意孤行要用DP的背包做这道题，于是 oh，一个STL的诡异容器从我的脑海中闪现了出来——映射 map ！

众所周知 map 进行一次操作的时间复杂度为 O(logn) 无疑会减慢运行速度，但是它省空间啊！（时间换空间，oh my god）于是就可以愉快地DP了！一次AC，秀一下这心惊胆战的提交记录：

（2018-08-06 10:59:20 修正，再次感谢ywk童鞋）各位reader们当我上面什么都没说……好像G的最大值推出来连1e5都没有……所以是存得下的。那么这道题就是一个简单的背包了！不需要map！

• 【源代码】

 /*Lucky_Glass*/
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<map>
 using namespace std;
 const int INF=int(1e9);
 int n,goal;
 int con[][];
 map<int,int>dp[];
 int DP(int x,int y)
 {
     if(y<=) return ;
     if(x<) return INF;
     if(dp[x].count(y)) return dp[x][y];
     dp[x][y]=INF;
     for(int i=;i<con[x][];i++)
         dp[x][y]=min(dp[x][y],DP(x-,y-i*x)+i);
     dp[x][y]=min(dp[x][y],DP(x-,y-con[x][]*x-con[x][])+con[x][]);
     return dp[x][y];
 }
 int main()
 {
     scanf("%d%d",&n,&goal);
     goal/=;
     for(int i=;i<=n;i++)
         scanf("%d%d",&con[i][],&con[i][]),con[i][]/=;
     printf("%d\n",DP(n,goal));
     return ;
 }

 (2018-08-06 11:01:03 修正代码)

 /*Lucky_Glass*/
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<map>
 using namespace std;
 const int INF=int(1e9);
 int n,goal;
 int con[][];
 int dp[][int(1e5)];
 int DP(int x,int y)
 {
     if(y<=) return ;
     if(x<) return INF;
     if(dp[x][y]!=-) return dp[x][y];
     dp[x][y]=INF;
     for(int i=;i<con[x][];i++)
         dp[x][y]=min(dp[x][y],DP(x-,y-i*x)+i);
     dp[x][y]=min(dp[x][y],DP(x-,y-con[x][]*x-con[x][])+con[x][]);
     return dp[x][y];
 }
 int main()
 {
     memset(dp,-,sizeof dp);
     scanf("%d%d",&n,&goal);
     goal/=;
     for(int i=;i<=n;i++)
         scanf("%d%d",&con[i][],&con[i][]),con[i][]/=;
     printf("%d\n",DP(n,goal));
     return ;
 }

◇D题◇ We Love ABC +传送门+

• 【题意】

给出一个字符串S，仅包含 'A','B','C'和'?' 。你可以（也必须）把'?'替换成'A'~'C'的任意一个字母，对于每一种替换全部完成的情况，计算满足下列条件的三元组（i,j,k）数量：

i<j<k，S[i]='A'，S[j]='B'，S[k]='C'。

统计总和。

• 【解析】

考虑没有'?'的情况，对于S的第i个字符，统计开头到第i-1个字符中A的个数（a[i]）以及从i+1到末尾C的个数（c[i]），若 S[i]='B'，则有 若选取第 i 个字符（作为中心的B），方案数为 a[i]*c[i] ，即 i 之前的每一个A都可以与 i 后面的C配对，形成一种答案（乘法原理）。所以我们只需要对 S 中的每一个B进行这样的一次计算，统计总和即可。

但是现在有'?'，我们再统计开头到i-1的'?'的数量（kn_fro[i]），以及从i+1到末尾'?'的数量（kn_beh[i]）。考虑下面3种情况：

(1) 将i之后的一个?变成C，与i前面的一个A配对，其余?任意变换。则配对的方案数为 a[i]*kn_beh[i]（乘法原理，前面的每一个A都可以与后面的每一个?配对），而其余?任意变换的方案数为 3^{kn_fro[i]+kn_beh[i]-1}，即剩余 (kn_fro[i]+kn_beh[i]-1)个?，每一个都可以换成 A~C 的任意一个。方案数为：

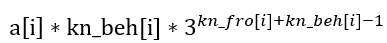
(2) 将i之前的一个?变成A，与后面的一个C配对，其余?任意变换……与(1)一样，方案为：

(3) 将i之前的一个?变成A，再把后面的一个?变成C，再将变换之后的A和C配对，其余乱选。选择A和C的方案为 (kn_fro[i]*kn_beh[i])，其他乱选的方案为(3^{kn_fro[i]+kn_beh[i]-2})——这次是有两个？已经固定，因此需要-2。方案数为：

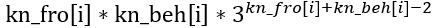
需要对哪些字符统计这样的值呢？

首先原来是B的字符一定要统计，当然还有每一个?，因为我们可以将那一个?固定变成B。

统计答案即可（标程好像是DP……我觉得没必要）

• 【源代码】

 /*Lucky_Glass*/
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 typedef long long ll;
 const ll MOD=ll(1e9)+;
 const int MAXN=int(1e5);
 ll Pow3[MAXN+];
 char S[MAXN+];
 ll a[MAXN+],c[MAXN+],kn_fro[MAXN+],kn_beh[MAXN+];
 int main()
 {
     ll f=;
     for(int i=;i<=1e5+;i++) Pow3[i]=f,f*=3ll,f%=MOD; //预处理3的次方
     scanf("%s",S);int len=strlen(S);
     for(int i=,totA=,totkn=;i<len;i++) //统计a[i],kn_fro[i]，均不包含第i个字符本身
     {
         a[i]=totA;kn_fro[i]=totkn;
         if(S[i]=='A') totA++;
         if(S[i]=='?') totkn++;
     }
     for(int i=len-,totC=,totkn=;i>=;i--) //统计c[i],kn_beh[i]，均不包含第i个字符本身
     {
         c[i]=totC;kn_beh[i]=totkn;
         if(S[i]=='C') totC++;
         if(S[i]=='?') totkn++;
     }
     ll ans=;
     for(int i=;i<len;i++)
         if(S[i]=='?' || S[i]=='B')
         { //这里一些玄学错误……如果大家发现只在第11组数据WA了，肯定是long long 炸了，把MOD的顺序换一下再交吧……
             ll O1=a[i]*((c[i]*Pow3[kn_beh[i]+kn_fro[i]])%MOD)%MOD, //A->C
                O2=kn_beh[i]? (a[i]*(kn_beh[i]*Pow3[kn_beh[i]+kn_fro[i]-]%MOD)%MOD):0ll, //A->?
                O3=kn_fro[i]? (c[i]*(kn_fro[i]*Pow3[kn_fro[i]+kn_beh[i]-]%MOD)%MOD):0ll, //?->C
                O4=(kn_beh[i] && kn_fro[i])? (kn_fro[i]*(kn_beh[i]*Pow3[kn_fro[i]+kn_beh[i]-]%MOD)%MOD):0ll; //?->?
             ll Sum=((O1+O2)%MOD+(O3+O4)%MOD)%MOD;
             ans+=Sum;
             ans%=MOD;
         }
     printf("%lld\n",ans);
     return ;
 }

---

◆ 涨Rating啦！

---

The End

Thanks for reading!

- Lucky_Glass

（Tab：如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我，在周末我会尽量解答并完善博客~）

dpij=mindpi-1j-k*100i+k(0≤k≤pi)dpij=mindpi-1j-k*100i-ci+k(k=pi)