2012年NOIP普及组 摆花

题目描述 Description

小明的花店新开张，为了吸引顾客，他想在花店的门口摆上一排花，共m盆。通过调查顾客的喜好，小明列出了顾客最喜欢的n种花，从1到n标号。为了在门口展出更多种花，规定第i种花不能超过ai盆，摆花时同一种花放在一起，且不同种类的花需按标号的从小到大的顺序依次摆列。

试编程计算，一共有多少种不同的摆花方案。

输入描述 Input Description

输入共2行。

第一行包含两个正整数n和m，中间用一个空格隔开。

第二行有n个整数，每两个整数之间用一个空格隔开，依次表示a1、a2、……an。

输出描述 Output Description

输出只有一行，一个整数，表示有多少种方案。注意：因为方案数可能很多，请输出方案数对1000007取模的结果。

样例输入 Sample Input

2 4

3 2

样例输出 Sample Output

2

数据范围及提示 Data Size & Hint

【输入输出样例说明】

有2种摆花的方案，分别是(1，1，1，2)，(1，1，2，2)。括号里的1和2表示两种花，比如第一个方案是前三个位置摆第一种花，第四个位置摆第二种花。

【数据范围】

对于20%数据，有0<n≤8，0<m≤8，0≤ai≤8；

对于50%数据，有0<n≤20，0<m≤20，0≤ai≤20；

对于100%数据，有0<n≤100，0<m≤100，0≤ai≤100。

算法分析

动态规划  （本文来自https://www.cnblogs.com/ssfzmfy/p/5793220.html）

题目要求花必须按从小到大的顺序摆放，并且同种类的花必须挨着放，则题目就简单多了

a[i]表示第i种花最多使用的盆数
f[i][j]表示前i种花，摆j盆的摆放方案数。

对于第i种花可以使用0、1、2...a[i]盆,对应的前i-1种花摆放的盆数为j-0、j-1、j-2、...j-a[i] 
即f[i][j]=f[i-1][j]+f[i-1][j-1]+f[i-1][j-2]+...+f[i-1][j-a[i]] =f[i-1][j-k](0<=k<=a[i],j>=k)
方程写出来后，最关键的就是赋初始值

初始值f[1][0]=1,f[1][1]=1,...f[1][a[1]]=1; 
初始值f[i][0]=1;(1<=i<=n)

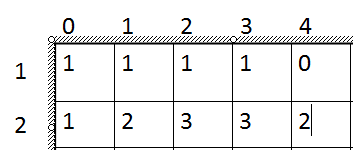
以题目的输入样例为例子手动推演如下：

2 4

3 2

 为例：

很显然f[1][1]=f[1][2]=f[1][3]=1;

f[2][1]=2,前2种花，放一盆，则有1,2两种方法。又

f[2][1]=f[1][0]+f[1][1]=f[1][0]+1可以推出f[1][0]=1；

同样的方法可以推出f[2][0]=f[3][0]=...=f[n][0]=1;

(f[2][2]=f[1][0]+f[1][1]+f[1][2]

f[2][3]=f[1][1]+f[1][2]+f[1][3]

f[2][4]=f[1][2]+f[1][3]+f[1][2])

 #include<iostream>
 #include<cstring>
 using namespace std;

 int f[][]={{,}};
 int a[];
 int main()
 {
     int n,m;
     cin>>n>>m;
     for(int i=;i<=n;i++) cin>>a[i];
     memset(f,,sizeof(f));

     for(int i=;i<=a[];i++) f[][i]=;
     for(int i=;i<=n;i++) f[i][]=;

     for (int i=;i<=n;i++)
         for(int j=;j<=m;j++)
             for(int k=;k<=a[i];k++)
                 if(j>=k) f[i][j]=(f[i][j]+f[i-][j-k])% ;
      cout<<f[n][m]<<endl;
     return ;
 }

方法2：初始值f[0][0]=1;前0种花摆放0盆的方案数为1

 //题目要求花必须按从小到大的顺序摆放，并且同种类的花必须挨着放，则题目就简单多了
 //f[i][j]表示前i种花，摆j盆的摆放方案数。对于第i种花可以使用0、1、2...a[i]盆,对应的前i-1种花摆放的盆数为j-0、j-1、j-2、...j-a[i]
 //即f[i][j]=f[i-1][j]+f[i-1][j-1]+f[i-1][j-2]+...+f[i-1][j-a[i]] (j>a[i])
 //初始值f[0][0]=1;前0种花摆放0盆的方案数为1
 //方程写出来后，最关键的就是赋初始值
 #include<iostream>
 #include<cstring>
 using namespace std;
 int f[][]={{,}};
 int a[];
 int main(){
     int n,m;
     cin>>n>>m;
     for(int i=;i<=n;i++) cin>>a[i];
     memset(f,,sizeof(f));
     f[][]=;
 //    for(int i=0;i<=a[1];i++) f[1][i]=1;
 //    for(int i=1;i<=n;i++)f[i][0]=1;
     for (int i=;i<=n;i++)
         for(int j=;j<=m;j++)
             for(int k=;k<=a[i];k++)
                 if (j>=k)f[i][j]=(f[i][j]+f[i-][j-k])% ;
     cout<<f[n][m]<<endl;
     return ;
 }

第二个方法的代码每太搞懂。。。